Problem 4. use the principle of induction to verify: $$\sum_{k=1}^n k^2 = \frac{n(n+1)(2n+1)}6$$
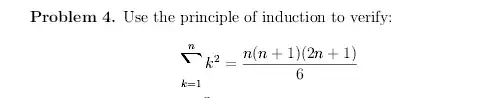
base case is obviously easy, but I don't know how to prove the inductive case
Problem 4. use the principle of induction to verify: $$\sum_{k=1}^n k^2 = \frac{n(n+1)(2n+1)}6$$
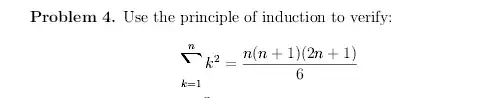
base case is obviously easy, but I don't know how to prove the inductive case
Hint:
$$\frac{n(n+1)(2n+1)}6+(n+1)^2=(n+1)\left(\frac{n(2n+1)}6+n+1\right)=$$
$$=(n+1)\left(\frac{n(2n+1)+6n+6}6\right)=\frac{n+1}6(n+2)(2n+3)\ldots\ldots$$
I'm pretty sure this has been answered before on this site, but anyway here's the proof:
$$\sum_{i=1}^n i^2 + (n+1)^2 = \frac{n(n+1)(2n+1)}{6} + (n+1)^2$$ $$\sum_{i=1}^{n+1} i^2 = \frac{n(n+1)(2n+1) + 6(n+1)^2}{6}$$ $$\sum_{i=1}^{n+1} i^2 = \frac{(n+1)((2n^2+n) + 6(n+1))}{6}$$ $$\sum_{i=1}^{n+1} i^2 = \frac{(n+1)(2n^2+7n+6)}{6}$$ $$\sum_{i=1}^{n+1} i^2 = \frac{(n+1)(2n+3)(n+2)}{6}$$ $$\sum_{i=1}^{n+1} i^2 = \frac{(n+1)(2(n+1)+1)((n+1)+1)}{6}$$