Why does $\int_1^\infty \sin(x \log x)\,\mathrm{d}x$ converge?

Question

Why does $\int_1^\infty \sin(x\log x)\,dx$ converge?

I haven't got a clue about where to being with this, any help would be appreciated.

Similar question posted here: http://math.stackexchange.com/questions/651951/does-the-integral-int-1-infty-sinx-log-x-mathrmdx-converge — Cardboard Box, Jan 29 '14 at 12:43
I've seen that question and was hoping someone could provide some clarity on the answer. — Mark Emacr, Jan 29 '14 at 12:47
If you've already found an answer and you don't understand it, you should open your question with that! And explain what you don't understand. — user37238, Jan 29 '14 at 12:55
The upshot is, by splitting the integral into pieces, you can write it as a convergent Alternating series. Drawing the graph of $f(x)=\sin(x\log x)$ should help here. — David Mitra, Jan 29 '14 at 12:57
In fact, this question has been duplicated many times. Why this is the one that gets closed - who knows. :) — Mark McClure, Jan 29 '14 at 13:32
Wolfram Alpha says no...
But this answer says yes! Looks like W|A is wrong on this one? — Bennett Gardiner, Jan 29 '14 at 13:45
@BennettGardiner Like Mathematica's Integrate command, W|A tests for absolute convergence. — Mark McClure, Jan 29 '14 at 14:10

Mark McClure · Accepted Answer · 2014-01-29T13:24:58.190

2

Let's take a look at a graph.

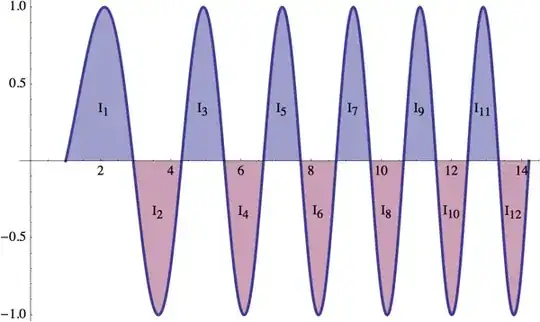
enter image description here

It appears that the graph oscillates up and down over the $x$-axis and that the labeled areas are decreasing to zero from left to right. In fact, it's not hard to prove these statements, namely

$$\int_1^\infty \sin(x\log x)\,dx = \sum_{n=1}^{\infty} (-1)^{n+1} I_n$$

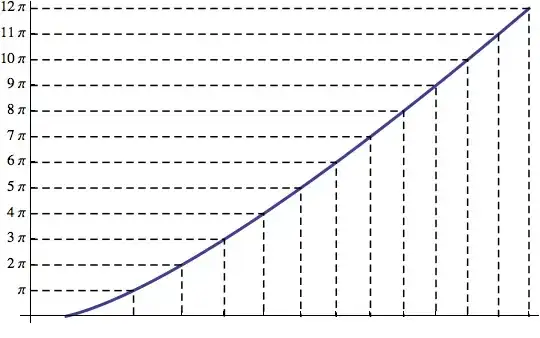
and that $\lim_{n\rightarrow\infty} I_n = 0$ with $0<I_{n+1}<I_n$. This boils down to the fact the area $I_k$ is bound on the left by the $k^\text{th}$ of $sin(x\log(x))$ and on the right by the next root. Furthermore, these roots are exactly the spots where $$x\log(x) = k\pi,$$ for some integer $k$. The fact that the distance between consecutive roots tends to zero boils down to the fact that $x\log(x)$ is an increasing, convex function.

enter image description here

edited Jan 29 '14 at 13:24

answered Jan 29 '14 at 13:07

Mark McClure

30,510

Thanks for this. Based on the answer that was linked, I need to prove that $I_n$ is a sign-alternating and monotonically decreasing in absolute value to zero (therefore giving me a Leibniz series which converges). I kind of understand how to show the sign-alternating, but have no idea how to show the monotonically decreasing in absolute value to 0. – Mark Emacr Jan 29 '14 at 13:14
@MarkEmacr I posted my answer prematurely since I saw the close votes coming. I hope the edit helps. – Mark McClure Jan 29 '14 at 13:27

Why does $\int_1^\infty \sin(x \log x)\,\mathrm{d}x$ converge?

1 Answers1