Suppose I have a (physical) template, consisting of a piece of stiff sheet plastic with a hole cut in the middle. Suppose the hole is in the shape of an ellipse, say, 8 x 12 inches. Suppose I then use a router (rotary cutter) that has a circular collar that rides against the edge of the template (inside the hole) and which has a rotary bit (like a truncated drill bit) that is 1/2" smaller than the diameter of the collar (1/4" smaller than the radius of the collar) and centered within it. If I attach the template to a flat surface and then use the router to cut a hole in that surface, keeping the collar tight against the inside edge of the template, will the resulting hole in the surface still be an ellipse?
Asked
Active
Viewed 378 times
3
-
Your router looks something like this, right? – J. M. ain't a mathematician Sep 15 '11 at 17:51
-
A related question. – J. M. ain't a mathematician Sep 15 '11 at 17:58
-
@J.M. -- Yep, essentially that kind of router. A collar would be fastened either to the base or to the shaft of the bit to hold the bit a fixed distance from the template edge. – Daniel R Hicks Sep 15 '11 at 18:41
-
@J.M -- I can't believe that I screwed up the title that badly!! I generally check spelling/wording over pretty closely, but after fixing the second "elipse" => "ellipse" I didn't look for the first, and the extra "d" must have fallen from the sky. – Daniel R Hicks Sep 15 '11 at 18:47
-
No worries. :) It's fixed now, right? – J. M. ain't a mathematician Sep 15 '11 at 18:56
-
Related: Uniform thickness border around skewed ellipse? – Nov 19 '12 at 18:19
1 Answers
4
If I understand correctly your description (I probably don't: my English drilling-related vocabulary is pretty nil!) the resulting curve will be a parallel curve to the ellipse, which is not an ellipse.
In the following picture, the outer curve is an ellipse with semiaxes $2$ and $1$, and the curves inside it are parallel curves to it, at distances separated $\tfrac1{10}$.
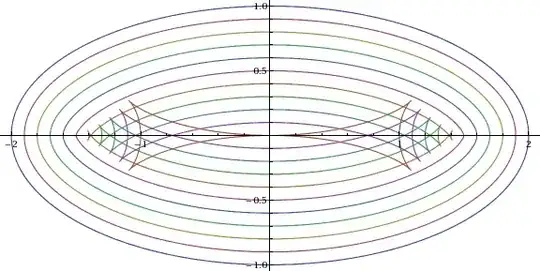
Technically, if $\alpha:(a,b)\to\mathbb R^2$ is a unit-speed parametrization of your curve oriented so that it has positive curvature (that is, so that it curves to the left), with its tangent vector $\mathbf T=\alpha'$ and its normal vector $\mathbf N$ (uniquely determined by the condition that $\{\mathbf T,\mathbf N\}$ be a positively oriented orthonormal basis of $\mathbb R^2$), then the parallel curve $\beta_d$ to $\alpha$ at distance $d$ in the direction of $\mathbf N$ is the curve $$\beta_d(t)=\alpha(t)+d \mathbf N(t).$$
Mariano Suárez-Álvarez
- 135,076
-
OK, thanks. I suspected as much, but my math is weak enough that I wasn't sure. And your diagram very nicely illustrates how it breaks down. – Daniel R Hicks Sep 15 '11 at 18:43