How to calculate with absolute value.

Question

Calculate:$$\frac{ \left| x \right| }{2}= \frac{1}{x^2+1}$$

How do I write the whole process so it will be correct? I need some suggestions. Thank you!

There are two cases: (1) $x\geq 0$ and (2) $x<0$. You could consider each separately. — pshmath0, Jan 20 '14 at 16:33
$\large x^{2} = \left\vert,x,\right\vert^{2}$ and you get a cubic equation for $\large\left\vert,x,\right\vert$. — Felix Marin, Jan 23 '14 at 16:48

score 15 · Accepted Answer · answered Jan 20 '14 at 16:33

15

Split it into two cases. First case is $$\frac{x}{2}=\frac{1}{x^2+1}.$$ If it has a positive solution (or more than one), it is a valid solution. Second case is $$\frac{-x}{2}=\frac{1}{x^2+1}.$$ If it has a negative solution (or more than one), then it is a valid solution.

The valid solutions from both cases are all your solutions to the original problem.

answered Jan 20 '14 at 16:33

Jeff Snider

2,817

2

so, you assume $x$ to be real? – lab bhattacharjee Jan 20 '14 at 16:34
6

I did because of the tags: calculus, and absolute-value. No mention of complex or modulus. – Jeff Snider Jan 20 '14 at 16:58

Macavity · Answer 2 · 2014-01-20T16:56:47.660

8

Let $y = \vert x \rvert \ge 0$. Then you have

$$y(y^2+1)=2 \implies y^3 +y - 2 = 0 \implies (y-1)(y^2+y+2)=0$$

The second factor cannot be zero for non-negative $y$, so you have only one solution $y=1 \implies x = \pm1$.

edited Jan 20 '14 at 16:56

answered Jan 20 '14 at 16:36

Macavity

46,381

1

+1 Doing cases $|x| = x$ or $|x| = -x$ is nice, but noting that $|x|^2 = x^2$ saves work at the end checking to make sure $x$ has the right sign. I like this answer best. – Caleb Stanford Jan 21 '14 at 03:42

lab bhattacharjee · Answer 3 · 2014-01-21T03:30:07.307

7

If $x=a+ib$ where $a,b$ are real

We have $$\frac{\sqrt{a^2+b^2}}2\left(a^2-b^2+2abi+1\right)=1$$

Equating the imaginary parts, $\displaystyle ab=0$

If $\displaystyle a=0, \frac{|b|}2(1-b^2)=1$

Use for real $b,|b|=\begin{cases} +b &\mbox{if } b\ge0 \\ -b & \mbox{if } b<0\end{cases}$

If $\displaystyle b=0, \frac{|a|}2(1+a^2)=1$

Set $x=r(\cos\phi+i\sin\phi)$ where $r>0, \phi$ are real

So using de Moivre's formula, $ x^2=r^2(\cos2\phi+i\sin2\phi)$

So we have $\displaystyle \frac r2\left(r^2(\cos2\phi+i\sin2\phi)+1\right)=1$

Equating the imaginary parts, $\displaystyle r^3\sin2\phi=0$

Clearly, $\displaystyle r\ne0\implies \sin2\phi=0\implies2\cos\phi\sin\phi=0$

If $\displaystyle\sin\phi=0, r^3+r-2=0$

Clearly, $r=1$ is a solution, so please solve the Quadratic Equation $\displaystyle\frac{r^3+r-2}{r-1}=0$

If $\displaystyle\cos\phi=0, r^3-r+2=0$ whose solution is not so smooth

edited Jan 21 '14 at 03:30

answered Jan 20 '14 at 16:33

lab bhattacharjee

274,582

I got only the following solutions (and none of them are real) $x=\frac{1}{2}(1-i\sqrt{7})$ and $x=\frac{1}{2}(1+i\sqrt{7})$. Is this even correct? – L_McClain Jan 20 '14 at 16:45
@L_McClain, I'm editing my answer – lab bhattacharjee Jan 20 '14 at 16:46
@ lab bhattacharjee, No, it's not that. I calculated on 2 different ways these x-es, and I only get imaginary solutions (?) – L_McClain Jan 20 '14 at 16:48
@L_McClain, how about $x=1$. Let me add the '-' sign – lab bhattacharjee Jan 20 '14 at 16:52
2

It's IMHO much easier to note that since the LHS is purely real, the RHS must be also, and so $x^2$ must be purely real; this means that either $x=r$ or $x=ri$ for some $r\in\mathbb{R}$, and these two cases can quickly be checked separately. – Steven Stadnicki Jan 20 '14 at 23:42
@StevenStadnicki, yes, I've added the derivation of that. – lab bhattacharjee Jan 21 '14 at 03:31

score 4 · Answer 4 · answered Jan 20 '14 at 16:34

4

By "calculuate", I presume you mean "solve for $x$". In that case, simply write two variations of the equation:

$$\frac{ x }{2}=\frac{1}{x^2+1}$$

and

$$\frac{ -x }{2}=\frac{1}{x^2+1}.$$

The solution set of you're original equation is the union of the solution sets of these two.

answered Jan 20 '14 at 16:34

Mark McClure

30,510

It is important that you note that in the first equation, x must be non-negative, and x must be negative for the second equation. Otherwise in a more complicated question you may introduce false solutions. – SimonT Jan 21 '14 at 00:03

score 2 · Answer 5 · answered Jan 20 '14 at 23:31

I'd like to offer a different approach to @labbhattacharjee's attempt to solve the equation over $\mathbb C$.

$$\frac{|x|}{2}=\frac{1}{x^2+1}$$

The left hand side is real, so at minimum the right hand side has to be real. The inverse of a real number is real, so $x^2+1$ is real, and the reals are closed under addition, so $x^2$ is real. Thus $x$ is either purely imaginary or purely real. The latter case has already been solved, and in the prior case, the equation reduces to:

$$\frac{|\Im(x)|}{2}=\frac{1}{-\Im(x)^2+1}$$

Which can presumably be solved for a real variable in much the same way as the original equation.

score 1 · Answer 6 · answered Jan 21 '14 at 03:35

Here's a plot of $\frac{ \left| x \right| }{2}-\frac{1}{x^2+1}$ in the complex plane (with corners at $-5-5i$ and $5+5i$):

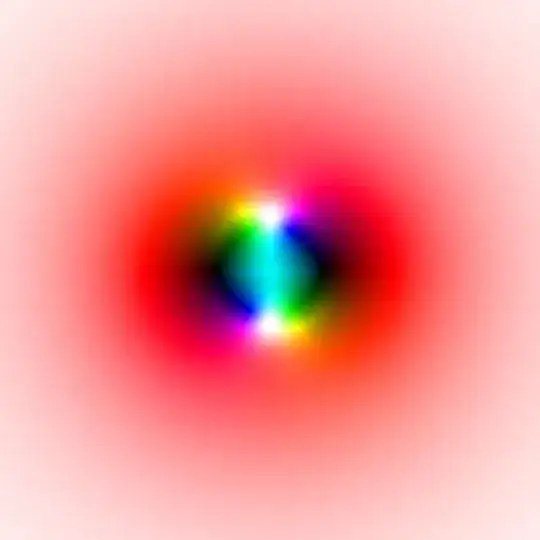
enter image description here

The zeros at $x=\pm 1$ are visible as black sinks. The colorizing is such that modulus is encoded as brightness and phase is encoded as hue. Not meant to be taken as a serious answer, but meant to be a visual supplement.

How to calculate with absolute value.

6 Answers6