a question about double integral

Question

Let $a,b$ be positive real numbers, and let $R$ be the region in $\Bbb R^2$ bounded by $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$. Calculate the integral $$ \int\int_R\left(1-\frac{x^2}{a^2}-\frac{y^2}{b^2}\right)^{3/2}dx\,dy $$

my question is I don't know anything about $R$, the function $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ is not the function of $R$, so then how can I get the answer? Could somebody give me some hints.

Answer 1

\begin{equation*}I=\iint_{R}(1-\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}})^{3/2}\,dx\,dy\tag{1} \end{equation*}

my question is I don't know anything about $R$

The equation \begin{equation*} \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\tag{2} \end{equation*} represents an ellipse centered at $(x,y)=(0,0)$, with major and minor axes coinciding with the $x,y$ axes. This ellipse is the boundary of the region $R$.

\begin{equation*}R=\left\{ (x,y)\in\mathbb{R}^{2}:0\le \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\le 1\right\}\tag{3}\end{equation*}

the function $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ is not the function of $R$

The integrand $(1-\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}})^{3/2}$ is evaluated over $R$.

To evaluate the integral $I$ we can proceed by making a transformation of the ellipse $(2)$ to a circle and then changing from cartesian to polar coordinates, or we could use right away polar coordinates.

• If we make the change of variables $x=aX,y=bY$, then we get the circle centered at $(X,Y)=(0,0)$ and radius $1$ \begin{equation*}X^{2}+Y^{2}=1.\tag{4}\end{equation*}The region $R$ becomes the unit circle \begin{equation*}C=\left\{ (X,Y)\in\mathbb{R}^{2}:0\le X^2+Y^2\le 1\right\}\tag{5}\end{equation*} The Jacobian determinant of the transformation is just \begin{equation*}\left\vert \frac{\partial (x,y)}{\partial (X,Y)}\right\vert =ab.\tag{6}\end{equation*} This corresponds to the following linear relation between the area elements\begin{equation*}dx\,dy=ab\,dX\,dY.\tag{7}\end{equation*}As a consequence the given integral over $R$ can be rewritten as an integral over $C$ \begin{equation*}I=\iint_{C}(1-( X^{2}+Y^{2}) )^{3/2}\,ab\,dX\,dY.\tag{8}\end{equation*}
• If we now use polar coordinates $r,\theta $ \begin{eqnarray*}X &=&r\cos \theta\\Y &=&r\sin \theta\\X^{2}+Y^{2}&=&r^{2}\tag{9}\end{eqnarray*} the integral $I$ becomes\begin{eqnarray*}I &=&ab\int_{r=0}^{1}\int_{\theta =0}^{2\pi }(1-r^{2})^{3/2}r\,dr\,d\theta\\ &=&2\pi ab\int_{0}^{1}(1-r^{2})^{3/2}r\,dr,\tag{10}\end{eqnarray*} because the Jacobian determinant \begin{equation*}\left\vert \frac{\partial (X,Y)}{\partial (r,\theta )}\right\vert =r.\tag{11}\end{equation*}In terms of area elements this means that they get converted by the relation \begin{equation*}dX\,dY=r\,dr\,d\theta .\tag{12}\end{equation*}
• Finally, to evaluate $I$ we can make the substitution $t=r^{2}-1$ \begin{equation*}I=2\pi ab\int_{0}^{1}(1-r^{2})^{3/2}r\,dr=2\pi ab\int_{0}^{1}\frac{1}{2}t^{3/2}\,dt=\frac{2ab}{5}\pi.\tag{13}\end{equation*}

Answer 2

Using $$x=ar\cos(t), y=br\sin(t),~~ 0\leq t\leq 2\pi,~r\ge0$$ we get $$\int_{t=0}^{2\pi}\int_{r=0}^1(1-r^2)^{3/2}J(x,y)drdt$$ For $J(x,y)$ look at this similar one Example2.

Answer 3

It sounds like you're just a bit confused about notation. $R$ is simply the name of the region. The notation

$$\iint\limits_{R} f(x,y) \, dA$$

simply means that we should integrate over the region $R$. In your case, $R$ is defined to be the region contained inside the ellipse

$$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1.$$

For $a=3$ and $b=2$, this situation could be illustrated as follows:

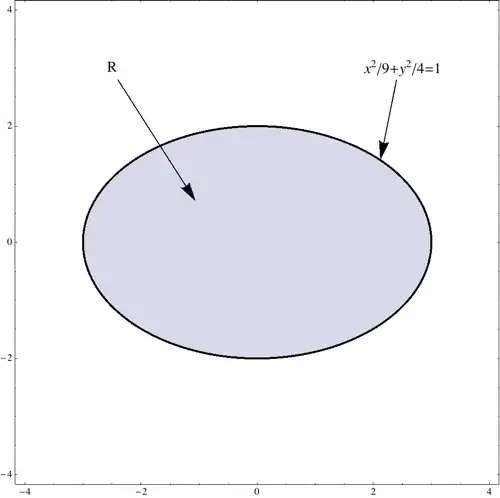
As the other answers already indicate, the integral can be evaluated easily by a change of variables $x=ar\cos(\theta)$ and $y=br\sin(\theta)$. It can also be expressed as an iterated integral in Cartesian coordinates

$$4\int_0^3 \int_0^{\frac{b}{a}\sqrt{a^2-x^2}} \left(1-\frac{x^2}{a^2} - \frac{y^2}{b^2}\right) \, dy \, dx,$$

which evaluates to $2\pi a b/5$, though it's certainly more algebraically cumbersome than the change of variables approach.