1

I tried to solve the limit. Please tell me if I did something wrong. (Because WolframAlpha gave me different answer) $$\lim_{x \to \infty}\frac{e^{\frac{1}{x^2}}-1}{2\arctan(x^2)-\pi}$$ Let $(u=\frac{1}{x}, x \to \infty, u\to 0)$: $$\lim_{u \to 0}\frac{e^{u^2}-1}{2\arctan\left(\frac{1}{u^{2}}\right)-\pi}=\lim_{u \to 0}\frac{u^2\ln(e)}{\left(\frac{2}{u^{2}}\right)-\pi}=\lim_{u \to 0}\frac{u^2}{\left(\frac{2}{u^{2}}\right)-\pi}=\lim_{u \to 0}\frac{u^2}{\frac{2- \pi\cdot u^2}{u^2}}=\lim_{u \to 0}\frac{u^4}{2-\pi \cdot u^2}=\frac{0}{2}=0$$

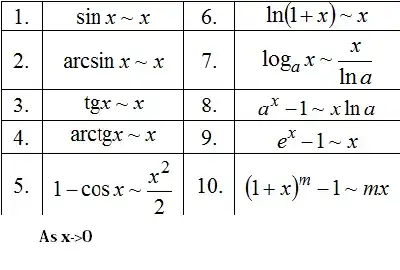
Note that I use these well-known rules: enter image description here

P.S: $\ln$ is natural logarithm

user91500
  • 5,606
k1ber
  • 507
  • 1
    I don't understand the second and third equalities that you have written above. Have you tried to use L'Hospital's rule? – voldemort Jan 17 '14 at 15:29
  • 2
    You set $\arctan \left(\frac{1}{u^2}\right) \leadsto \frac{1}{u^2}$, but $\arctan x \sim x$ is only valid for $x$ close to $0$. For $u$ close to $0$, $\frac{1}{u^2}$ is close to $\infty$. – Daniel Fischer Jan 17 '14 at 15:29
  • @voldemort, no, I haven't. I'd like to solve this limit without L'Hospital's – k1ber Jan 17 '14 at 15:34
  • @DanielFischer, thanks, I have not noticed that fact. – k1ber Jan 17 '14 at 15:36

1 Answers1

3

If $u >0$, then $\displaystyle\arctan\left(\frac1u\right)= \frac{\pi}{2}-\arctan(u)$. Let $u =\displaystyle\frac1{x^2}$. The given problem becomes

$$\displaystyle \lim_{u \to 0^+} \frac{e^u-1}{2\arctan\left(\frac1u\right)-\pi} =-\frac{1}{2}\lim_{u\to0^+}\frac{e^u-1}u\cdot\lim_{u\to0^+}\frac{u}{\arctan(u)}.$$

The last two limits are easily seen to be $1$ by L'Hospital's Rule. So the answer is $\displaystyle-\frac{1}{2}.$

some person
  • 186
lab bhattacharjee
  • 274,582
  • In your last step, can we use the fact that $arctan(u) = u,as u \to 0$? – k1ber Jan 17 '14 at 15:43
  • @KiberPrestupnik, what is $\tan(0)$? – lab bhattacharjee Jan 17 '14 at 15:44
  • I think it's zero. But I don't understand what do you mean – k1ber Jan 17 '14 at 15:46
  • @KiberPrestupnik, $\lim_{x\to a}f(x)=f(a)$ – lab bhattacharjee Jan 17 '14 at 15:47
  • @KiberPrestupnik, but please don't miss out the first formula with "x>0" – lab bhattacharjee Jan 17 '14 at 15:57
  • Ok, thanks for your help. But I have only one question left. Why can't we use these rules from the picture http://i.stack.imgur.com/knAfZ.png Then (as I think) we could get $1\cdot\frac1{-2\lim_{u \to 0^+}\frac{\arctan u}u}=1\cdot\frac1{-2\lim_{u \to 0^+}\frac{u}u}=1\cdot\frac1{-2}=-\frac{1}{2}$ – k1ber Jan 17 '14 at 15:59
  • @KiberPrestupnik, definitely, you can. But in some Questions needs without using L'Hospital Rule or Series Expansion like http://math.stackexchange.com/questions/387333/are-all-limits-solvable-without-lhospital-rule-or-series-expansion – lab bhattacharjee Jan 17 '14 at 16:02