What is completing the square?

Question

Why is it called, completing the square? Is square metaphorical in this sense? How do you complete the square and what is it used for?

Thank you, regards.

Answer 1

Suppose you have an expression like $x^2+ax+b$. For some purposes you might want it to have a form of a square, like $(x+q)^2$. Square is not metaphorical here, it refers to a power of 2.

Now, how do we accomplish this? First, expand the square: $$(x+q)^2=x^2+2xq+q^2.$$

We can see that our $ax$ can be what is $2xq$ here, so $q=\frac{a}2$. Now our expression becomes $$(x+q)^2=x^2+ax+\left(\frac{a}2\right)^2.$$ Compare it with original formula, see that it is almost a square if not this term: $C=\left(\frac{a}2\right)^2-b$. So we just add it and thus complete the square:

$$x^2+ax+b+C=x^2+ax+b+\left(\frac{a}2\right)^2-b=\left(x+\frac{a}2\right)^2$$

Now our expression has become a complete square.

Answer 2

Consider the quadratic term $x^2+2x-11$. The goal of completing the square is to write this term in a form where $x$ appears only once and the idea behind this is to use the binomial formula $(a+b)^2=a^2+2ab+b^2$ in opposite direction. So we set $a=x$ and then it looks like $2ab$ should be $2x$ and since $a=x$ we get $2xb=2x$ which gives us $b=1$. Then $$(x+1)^2=x^2+2x+1^2=x^2+2x+1.$$ But wait a minute, we want $x^2+2x-11$. What do we do? We add the missing $1$ to complete the square: \begin{align} x^2+2x-11 &= x^2+2x+1-1-11 \\ &= (x+1)^2-1-11 \\ &= (x+1)^2-12. \end{align}

Answer 3

Please forgive my poor mspaint skills. On the left, I've represented a quadratic by drawing its square part, its linear part, and some left over constant parts. On the right, we've chopped the linear part in half and reassembled things into a larger square with some left over constant parts, but no linear part.

I have no idea if the actual etymology has any resemblance to this.

Answer 4

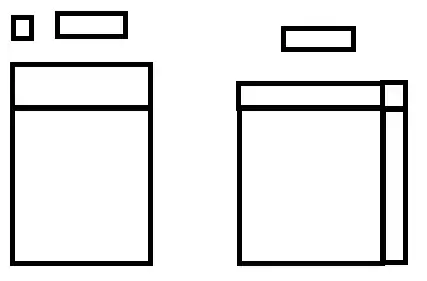
Here are an approach that is similar to the one I use to teach the concept to my own students. (I generally do this with a quadratic of the form $x^2+bx+c,$ as it simplifies the arguments, and the more general case can be scaled at the beginning and end to work similarly.)

Note that if we start with a general quadratic $ax^2+bx+c,$ we could picture it as the total volume of three box-shaped solids with the following respective dimensions:

• $a\times x\times x,$
• $1\times b\times x,$
• $1\times c\times 1.$

This makes things slightly more complicated to draw, though, so as an alternative, letting $b'=\frac ba$ and $c'=\frac ca,$ we will instead consider it as the total volume of three box-shaped solids with the following dimensions:

• $a\times x\times x,$
• $a\times b'\times x,$
• $a\times c'\times 1.$

Putting the first two together and leaving the third floating loose, we obtain two box-shaped solids having height $a,$ with bases having the following respective dimensions:

• $x\times(x+b'),$
• $c'\times 1.$

Since we're considering only box-shaped solids with the same height, then the bases of the solids pretty much tell us the whole story about their total volume (and are easier to draw than the $3$-dimensional alternative):

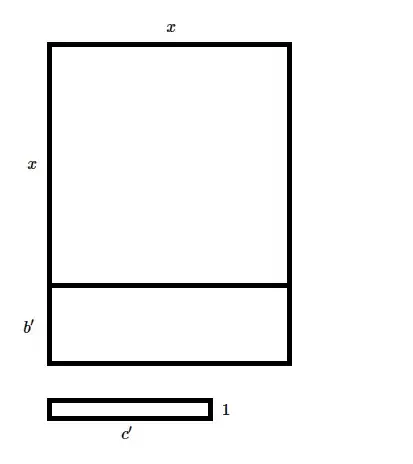
Now, let's split the solid with the $b'\times x$ base into two solids with bases of dimension $\frac{b'}2\times x.$ This gives us:

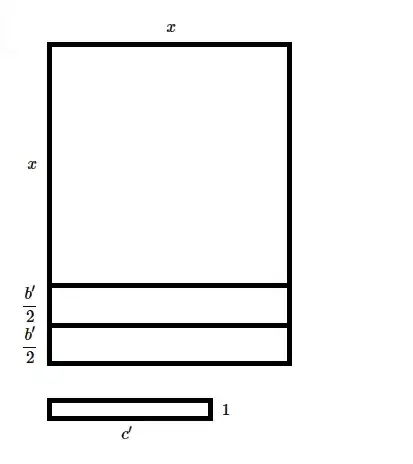
Now, let's slide one of the two solids we've made around to the right side of our solid with the $x\times x$ base. This gives us:

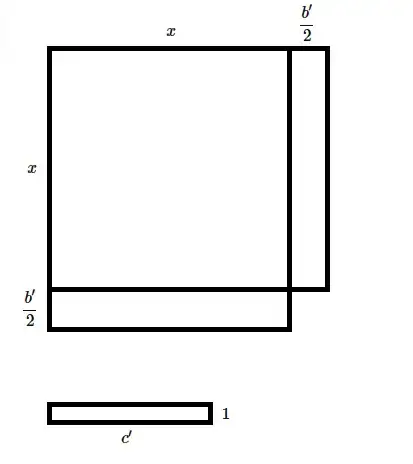
Now, we're very close to having a box-shaped solid with a square base of dimension $\left(x+\frac{b'}2\right)\times\left(x+\frac{b'}2\right)$ (together with a floating box-shaped solid of the same height), but the square-based box-shaped solid isn't quite complete. All that is missing is a box-shaped solid of height $a$ with base dimensions $\frac{b'}2\times\frac{b'}2.$ To obtain the missing portion, we will remove a box-shaped solid of dimensions $a\times\left(\frac{b'}2\right)^2\times 1$ from the floating box-shaped solid, leaving a box-shaped solid with dimensions $a\times\left(c'-\left(\frac{b'}2\right)^2\right)\times 1,$ then we will reshape the removed box-shaped solid into a box-shaped solid of dimensions $a\times\frac{b'}2\times\frac{b'}2.$ This reshaped solid fits nicely into the missing corner, giving us:

So, we subtracted from the floating solid (which represented the constant term) and added what we took onto the other solid to complete the square-based box-shaped solid (which began as the sum of our other two terms).

Answer 5

ok so you are talking about some equation or?for example let us take following situation

http://www.purplemath.com/modules/sqrquad.htm

from there we can easily guess that we may need several easy algebraic equation so that solve easily task,example

$x^2+6*x=18$

let us do following algebraic term

$x^2+6*x+9=18+9$

now

$x^2+6*x+9=(x+3)^2$

and finally we get

$(x+3)^2=27$

do you see point?