1

This example is from Paul's Online Notes for Calc I.

You have $500$ feet of fencing material and you want to enclose a field with a fence. A building is on one side of the field (and so won't need any fencing). Determine the dimensions of the field that will enclose the largest area.

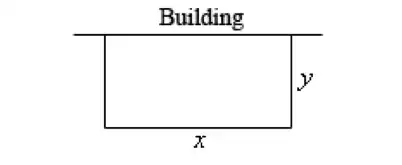
enter image description here

Maximize: $\;\;\;A=xy$
Constraint: $\;\;\;500=x+2y$

$x=500-2y \implies A(y)=(500-2y)(y) \implies A(y)=500y-2y^2$

Then, for determining the interval, he states:

Now we want to find the largest value this will have on the interval [$0,250]$. Note that the interval corresponds to taking $y=0$ (i.e. no sides to the fence) and $y=250$ (i.e. only two sides and no width, also if there are two sides each must be $250$ ft to use the whole $500$ft).

My Questions:

$\textbf{1.}\;\;$ I don't understand his explanation for determining the interval...why is he considering no sides to the fence, which he labels as $y=0$, and only two sides and no width, which he labels as $y=250$? It seems like these numbers come from $2y(250-y) \implies y=0, y=250$, but I still don't understand why this is the case. How can you ignore dimensions when determining the domain?

$\textbf{2.}\;\;$ How do you know that the largest area will be rectangular? Why doesn't he choose to maximize a circle or square, for example?

Thanks.

Emi Matro
  • 5,013

3 Answers3

1

1. The two cases are just theoretical and will yield to some kind of degenerated rectangles, such that the surface of the domain is equal to zero. You could also chose (for the one case) $y=\epsilon$ for some very small $\epsilon$. The smaller you chose $\epsilon$ the smaller the surface will get, but it can't be smaller than $0$ wich would be the case for $\epsilon=0$.

2. Indeed this is not clear but the auther apparently is asking for the largest rectangle. Your question is coherent, the task is not well formulated.

user127.0.0.1
  • 7,267
1

The second point first... your objection is perfectly sensible, and if Paul only wanted to consider rectangles, he should have said so in the question. In fact, forming the fence into a circle - or to be more precise, a semicircle - will give a larger area. (A square, on the other hand, is a special kind of rectangle and therefore is not excluded by Paul's method of solution, though it doesn't happen to be the right answer in this case.)

The restrictions on $y$ arise from considering the physical meaning of the problem. You can't (in this question) have a length less than zero for the vertical side, so the minimum possibility is $y=0$. You can't have a length less than zero for the horizontal side either, and a little thought will show you that this means $y$ can't be greater than $250$.

I think perhaps you are not recognising that "no sides to the fence" is different from "sides of length zero".

David
  • 82,662
1

  1. He wants x and y to both be nonnegative, so $y\ge0$, and $x\ge0\iff 500-2y\ge0\iff y\le250$. This gives him the domain $[0,250]$, but he is only including the endpoints for convenience. It is more realistic to take the domain to be $(0,250)$.

  2. He is assuming in the problem, although he didn't state this explicitly, that the field is rectangular.

user84413
  • 27,211