I have vector u=(x,y) and i need to create matrix M: M*u=(1,0).
But that matrix has to rotate vector, instead of keep and scale the x unit. So when i apply it on different vectors, the angle between them won't change.
Btw, this isn't homework! We haven't learned any matrices at school yet. ;)
Your problem is equivalent to find the transformation between the $x,y$ coordinates of a point and the $x^{\prime },y^{\prime }$ coordinates of the same point in a rotated system of coordinates, followed by a multiplication by the factor $k=1/\sqrt{x^{2}+y^{2}}$, so that $x^{\prime \prime }=kx^{\prime }=1$ and $y^{\prime \prime }=kx^{\prime }=0$. The rotation angle should be $\theta =\arctan \frac{y}{x}$.
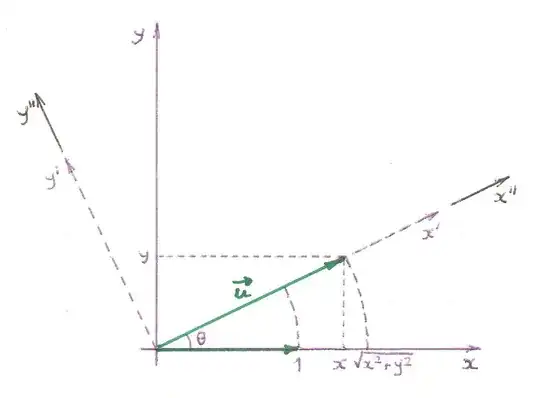
From trigonometry, we know that
$$ \begin{eqnarray*} &&\left\{ \begin{array}{c} x^{\prime }=x\cos \theta +y\sin \theta =\sqrt{x^{2}+y^{2}} \\ y^{\prime }=-x\sin \theta +y\cos \theta =0 \end{array} \right. \end{eqnarray*} $$ and since
$$ \begin{eqnarray*} \cos \left( \arctan \frac{y}{x}\right) &=&\frac{x}{\sqrt{x^{2}+y^{2}}} \\ \sin \left( \arctan \frac{y}{x}\right) &=&\frac{y}{\sqrt{x^{2}+y^{2}}}, \\ \end{eqnarray*} $$
we have $$\begin{eqnarray*} \left\{ \begin{array}{c} x^{\prime \prime }=\frac{1}{\sqrt{x^{2}+y^{2}}}x^{\prime }=\frac{x^{2}}{ x^{2}+y^{2}}+\frac{y^{2}}{x^{2}+y^{2}}=1 \\ y^{\prime \prime }=\frac{1}{\sqrt{x^{2}+y^{2}}}y^{\prime }=-\frac{xy}{ x^{2}+y^{2}}+\frac{xy}{x^{2}+y^{2}}=0. \end{array} \right. \end{eqnarray*} $$
We haven't learned any matrices at school yet.
In matrix notation$^1$
$$ \begin{eqnarray*} \begin{pmatrix} x^{\prime \prime } \\ y^{\prime \prime } \end{pmatrix} &=&\frac{1}{\sqrt{x^{2}+y^{2}}} \begin{pmatrix} x^{\prime } \\ y^{\prime } \end{pmatrix} = \begin{pmatrix} \frac{x}{x^{2}+y^{2}} & \frac{y}{x^{2}+y^{2}} \\ -\frac{y}{x^{2}+y^{2}} & \frac{x}{x^{2}+y^{2}} \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \end{pmatrix}. \end{eqnarray*} $$
So $$ M= \begin{pmatrix} \frac{x}{x^{2}+y^{2}} & \frac{y}{x^{2}+y^{2}} \\ -\frac{y}{x^{2}+y^{2}} & \frac{x}{x^{2}+y^{2}} \end{pmatrix}. $$
--
$^1$ Product of a $2\times 2$ matrix by a $2\times 1$ matrix $$ \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix} \begin{pmatrix} b_{1} \\ b_{2} \end{pmatrix} = \begin{pmatrix} a_{11}b_{1}+a_{12}b_{2} \\ a_{21}b_{1}+a_{22}b_{2} \end{pmatrix} $$
and product between a scalar $\alpha$ and a $2\times 1$ matrix
$$\alpha \begin{pmatrix} c_{1} \\ c_{2} \end{pmatrix} = \begin{pmatrix} \alpha c_{1} \\ \alpha c_{2} \end{pmatrix} $$
I assume you want a 2$\times$2 rotation matrix that sends $\vec{u}=(x,y)$ to $\vec{e}_1=(1,0)$. (The question is a bit unclear in my opinion: what does it mean to "keep and scale the x unit"? Isn't that an oxy-moron? I assume you want to preserve angles under transformation, i.e. $\angle\vec{a}\vec{b}=\angle(M\vec{a})(M\vec{b})$, right?) The dot product's angle formula gives $\cos\theta=\vec{u}\cdot\vec{e_1}/r$, where $\theta$ is the angle from $\vec{e}_1$ to $\vec{u}$ and $r=\|\vec{u}\|=\sqrt{x^2+y^2}$ is the magnitude. Now we use this to find the entries of the rotation matrix $R(-\theta)$ (the matrix transforms counterclockwise normally, so to get it to go backwards we need to negate the angle sign); see the Wikipedia link. Note $\sin^2+\cos^2=1$. Moreover, we have to divide this rotation matrix by another $r$ so that it scales down $\vec{u}$ to unit size. Thus we have
$$M=\begin{pmatrix}x/r^2&y/r^2\\-y/r^2&x/r^2\end{pmatrix}.$$
You can check that this indeed sends $\vec{u}$ to $\vec{e}_1$.
