Formula to project a vector onto a plane

Question

I have a reference plane formed by $3$ points in $\mathbb{R}^3$ – $A, B$ and $C$. I have a $4$th point, $D$. I would like to project the vector $\vec{BD}$ onto the reference plane as well as project vector $\vec{BD}$ onto the plane orthogonal to the reference plane at vector $\vec{AB}$. Ultimately, I need the angle between $\vec{AB}$ and $\vec{BD}$ both when the vectors are projected on to the reference plane as well as the orthogonal plane. I have completed tutorials on projecting a vector onto a line in $\mathbb{R}^2$ but haven't figured out how to translate that to $\mathbb{R}^3$...

Please note the diagram only shows the reference plane as parallel to the $xy$ plane for the sake of convenience. In my examples, the reference plane could be at any orientation. I am using $3$D coordinate data from an electromagnetic motion tracker and the reference plane will be constantly moving. I understand the cross product of the two vectors $\vec{AB} \times \vec{BC}$ results in the normal vector to their plane. I have $2$ different methods to calculate that but am a little lost once I get to this point. I have seen both unit vector notation and column vector notation but am confused by moving between the different styles. It would be most helpful if you could tell me the formal name of the notation/equations you use. I know the scalar equation of a plane through point $(a,b,c)$ with normal $\hat{n} = [n_1, n_2, n_3]$ is:
$$ n_1(x-a) + n_2(y-b) +n_3(z-c) = 0 $$ and the standard linear equation definition is: $$ Ax + By + Cz = D $$ but I could use some tips on when the equation is $=D$ and when it is $=0$ as well as any additional equations for a plane and in which circumstances the different forms are appropriate. I hope I've made sense here. Thanks for any help you can provide.

Answer 1

If $A$,$B$,$C$ are not on the same line, then $\vec{AB}\times \vec{BC}$ will give you the direction of your reference plane normal vector $\hat{n}_1$. I think you should know how to do the normalization so that $|\hat{n}_1|=1$

Then the projection of $\vec{BD}$ on the reference plane is $\vec{BD}-(\vec{BD}\cdot \hat{n}_1)\hat{n}_1$

Another plane $\hat{n}_2$ orthogonal to the reference plane ABC can be found as $\vec{AB}\times\hat{n}_1$ (again you need to normalize it). Then the projection of $\vec{BD}$ on that plane can alsow be found in a similar way as shown for the first plane.

Answer 2

1. Obtain the equation of the reference plane by ${\bf n}:=\vec{AB}\times\vec{AC}$, the left hand side of equation will be the scalar product ${\bf n}\cdot{\bf v}$ where $\bf v$ is the (vector from origin to the) variable point of the equation, and the right hand side is a constant, such that e.g. ${\bf v}=A$ has to satisfy it, that is, the equation will be

${\bf n}\cdot{\bf v}={\bf n}\cdot A\,$. 2. Calculate orthogonal and parallel components of $\vec{BD}$ relative to $\bf n$: we look for vectors $\vec{BD}_\perp$ and $\vec{BD}_\| $ such that $\vec{BD}=\vec{BD}_\perp+\vec{BD}_\| $, $\ \vec{BD}_\perp\ \perp\ {\bf n}$ and $\ \vec{BD}_\| \,\parallel\,{\bf n}$.
That means, $\vec{BD}_\|=\lambda{\bf n}$ for some $\lambda\in\Bbb R$ and $\vec{BD}_\perp\cdot{\bf n}=0$. Using this and scalar multiplying by $\bf n$: $$\vec{BD}\cdot{\bf n}=0+\lambda\cdot{\bf n}^2$$ this enables you to compute $\lambda$, hence $\vec{BD}_\|$ then $\vec{BD}_\perp:=\vec{BD}-\vec{BD}_\|$. 3. Do the same for the other reference plane, (one of) its normal vector will be ${\bf n}\times\vec{AB}$. 4. The angle $\varphi$ of vectors ${\bf u}$ and ${\bf v}$ can be calculated by the following formula: $$\cos\varphi=\frac{{\bf u}\cdot{\bf v}}{\Vert{\bf u}\Vert\,\Vert{\bf v}\Vert} \,.$$

Answer 3

Let the displacement of $\mathbf{\vec{{v}_{0}{v}_{1}}}$ be a directed vector from $\mathbf{\vec{v}_{0}}$ to $\mathbf{\vec{v}_{1}}$ defined as $\left(\mathbf{\vec{v}_{1}}-\mathbf{\vec{v}_{0}}\right)$.

$$\mathtt{\operatorname{Let }}\mathbf{V=\left\{\vec{a},\vec{b}\right\}};$$

"Let $\operatorname{Ortho}_{\mathbf{\vec{b}}}\left(\mathbf{\vec{a}}\right)$ be the orthogonalization of $\mathbf{\vec{a}}$ compared to $\mathbf{\vec{b}}$ about $\mathbf{\vec{0}}$."

$ \mathbf{\forall\vec{a}\forall\vec{b}}\left(\text{Ortho}_{\mathbf{\vec{b}}}\left(\mathbf{\vec{a}}\right)=\mathbf{\vec{a}}-\text{Proj}_{\mathbf{\vec{b}}}\left(\mathbf{\vec{a}}\right)\implies\mathbf{\forall\vec{v}}\left(\pm\left(\mathbf{\vec{a}}\times\mathbf{\vec{b}}\right)\cdot\mathbf{\vec{v}}=\mathrm{0}\land\mp\left(\mathbf{\vec{b}}\times\mathbf{\vec{a}}\right)\cdot\mathbf{\vec{v}}=\mathrm{0}\land\mathbf{\vec{v}}\in\mathbf{V}\implies\text{Ortho}_{\mathbf{\vec{b}}}\left(\mathbf{\vec{a}}\right)\cdot\mathbf{\vec{v}}=0\land\left(\mathbf{\vec{v}}\in\mathbb{R}^3\implies\text{Ortho}_{\mathbf{\vec{b}}}\left(\mathbf{\vec{a}}\right)\in\mathbb{R}^3\right)\right)\right) $

"Let $\text{Proj}_{\mathbf{\vec{b}}}\left(\mathbf{\vec{a}}\right)$ be the (linear) projection of $\mathbf{\vec{a}}$ onto $\mathbf{\vec{b}}$ about $\mathbf{\vec{0}}$."

$ \mathbf{\forall\vec{a}\forall\vec{b}}\left(\text{Proj}_{\mathbf{\vec{b}}}\left(\mathbf{\vec{a}}\right)=\frac{\mathbf{\vec{a}}\cdot\mathbf{\vec{b}}}{\mathbf{\vec{b}}\cdot\mathbf{\vec{b}}}\mathbf{\vec{b}}\land\mathbf{\vec{b}}\not=\mathbf{\vec{0}}\land\frac{\pi}{2}= \arccos⁡\left(\frac{\left(\mathbf{\vec{a}}-\text{Proj}_{\mathbf{\vec{b}}}\left(\mathbf{\vec{a}}\right)\right)\cdot\left(\mathbf{\vec{b}}-\text{Proj}_{\mathbf{\vec{b}}}\left(\mathbf{\vec{a}}\right)\right)}{\Vert\mathbf{\vec{a}}-\text{Proj}_{\mathbf{\vec{b}}}\left(\mathbf{\vec{a}}\right)\Vert \Vert\mathbf{\vec{b}}-\text{Proj}_{\mathbf{\vec{b}}}\left(\mathbf{\vec{a}}\right)\Vert}\right)\land\left(\mathbf{\vec{b}}\in\mathbb{R}^n\land\mathbf{\vec{a}}\in\mathbb{R}^n\land\mathbf{\vec{0}}\in\mathbb{R}^n\implies\text{Proj}_{\mathbf{\vec{b}}}\left(\mathbf{\vec{a}}\right)\in\mathbb{R}^n\right)\right) $

The formula to project a vector onto a plane.

"Let $\vec{F}\left(\mathbf{\vec{v}},i,\mathbf{\vec{X}}_{i,j}\right)$ be the orthogonalization of $\mathbf{\vec{v}}$ compared to $\mathbf{\vec{X}}_{i,1}$ about $\mathbf{\vec{X}}_{i,2}$."

$ \therefore\forall \mathbf{\vec{v}}\exists\mathbf{\vec{X}}\left(\mathbf{\vec{X}}\in\left\{\mathbf{\vec{R}_{\mathbf{V}}\left(P\right)},\mathbf{\vec{O}_{\mathbf{V}}\left(P\right)}\right\}\implies\vec{F}\left(\mathbf{\vec{v}},i,\mathbf{\vec{X}}_{i,j}\right)=\mathbf{\vec{v}}-\text{Proj}_{\left(\mathbf{\vec{X}}_{i,1}-\mathbf{\vec{X}}_{i,2}\right)}\left(\mathbf{\vec{v}}-\mathbf{\vec{X}}_{i,2}\right)\right) $

the traced codomain of $\vec{F}$ of a traced random $\mathbf{\vec{v}}$ about one instance of $\mathbf{\vec{X}}$.

---

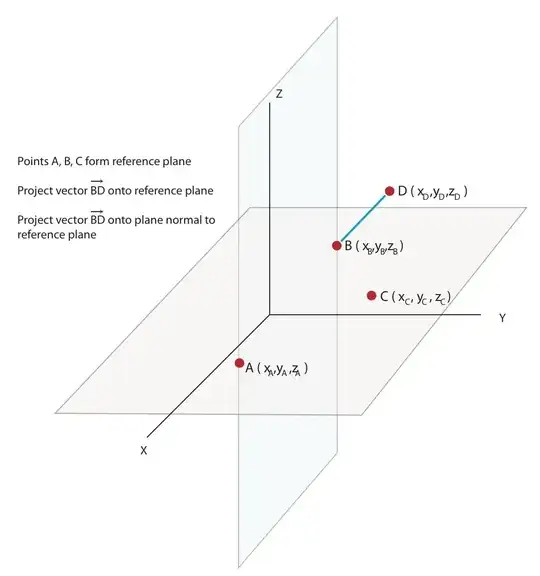
"A reference plane formed by 3 points in $\mathbb{R}^3$."

Let plane $\mathbf{P}$ be a binary tuple of a normal constructor $\vec{\text{C}}$ using planer point(s) $\mathbf{\vec{p}}\in\mathbf{V}$:

$\mathbf{P}= \left(\vec{\text{C}}\left(\mathbf{\vec{p}}\right),\mathbf{\vec{p}}\right)\iff\left(\mathbf{\vec{n}}=\vec{\text{C}}\left(\mathbf{\vec{p}}\right)\implies \mathbf{P}\overset{\text{def}}{=}\forall\mathbf{\vec{v}}\left(\left(\mathbf{\vec{n}}-\mathbf{\vec{0}}\right)\cdot\left(\mathbf{\vec{v}}-\mathbf{\vec{p}}\right)=0\right)\right);$

$\mathtt{\text{Let }}\mathbf{V}=\left\{\vec{A},\vec{B},\vec{C}\right\};$

Let $\mathbf{\vec{R}_{\mathbf{V}}\left(P\right)}$ is an array data structure that contains all possible implementations of planes using all vectors in $\mathbf{V}$ given $\mathbf{P}$. $$ \mathtt{\text{Let }}\mathbf{\vec{R}_{\mathbf{V}}\left(P\right)}= \begin{bmatrix} \left(\frac{(\vec{A}-\vec{C}) \times (\vec{B}-\vec{C})}{\Vert(\vec{A}-\vec{C}) \times (\vec{B}-\vec{C})\Vert}+\vec{C}, \vec{C}\right) \\ \left(\frac{(\vec{A}-\vec{B}) \times (\vec{C}-\vec{B})}{\Vert(\vec{A}-\vec{B}) \times (\vec{C}-\vec{B})\Vert}+\vec{B}, \vec{B}\right) \\ \left(\frac{(\vec{B}-\vec{A}) \times (\vec{C}-\vec{A})}{\Vert(\vec{B}-\vec{A}) \times (\vec{C}-\vec{A})\Vert}+\vec{A}, \vec{A}\right) \\ \left(\frac{(\vec{B}-\vec{C}) \times (\vec{A}-\vec{C})}{\Vert(\vec{B}-\vec{C}) \times (\vec{A}-\vec{C})\Vert}+\vec{C}, \vec{C}\right) \\ \left(\frac{(\vec{C}-\vec{B}) \times (\vec{A}-\vec{B})}{\Vert(\vec{C}-\vec{B}) \times (\vec{A}-\vec{B})\Vert}+\vec{B}, \vec{B}\right) \\ \left(\frac{(\vec{C}-\vec{A}) \times (\vec{B}-\vec{A})}{\Vert(\vec{C}-\vec{A}) \times (\vec{B}-\vec{A})\Vert}+\vec{A}, \vec{A}\right) \end{bmatrix}; $$

Example: $$\mathbf{\vec{R}_{\mathbf{V}}\left(P\right)}_{2}=\mathbf{\vec{R}_{\mathbf{V}}\left(P\right)}_{2,j}=\left(\frac{(\vec{A}-\vec{B}) \times (\vec{C}-\vec{B})}{\Vert(\vec{A}-\vec{B}) \times (\vec{C}-\vec{B})\Vert}+\vec{B}, \vec{B}\right);$$ $$\mathbf{\vec{R}_{\mathbf{V}}\left(P\right)}_{2,1}=\frac{(\vec{A}-\vec{B}) \times (\vec{C}-\vec{B})}{\Vert(\vec{A}-\vec{B}) \times (\vec{C}-\vec{B})\Vert}+\vec{B};$$

$$\mathbf{\vec{R}_{\mathbf{V}}\left(P\right)}_{2,2}=\vec{B};$$

"The plane orthogonal to the reference plane at $\vec{AB}$."

Let $\mathbf{\vec{O}_{\mathbf{V}}\left(P\right)}$ inherit the definition of $\mathbf{\vec{R}_{\mathbf{V}}\left(P\right)}$, but redefines the normal constructor $\vec{\text{C}}\left(\mathbf{\vec{p}}\right)$ implemented in $\mathbf{\vec{R}_{\mathbf{V}}\left(P\right)}$. $$ \mathtt{\text{Let }}\mathbf{\vec{O}_{\mathbf{V}}\left(P\right)} = \begin{bmatrix} \left(\frac{\left(\mathbf{\vec{R}_{\mathbf{V}}\left(P\right)}_{2,1}-\vec{B}\right)\times(\vec{A}-\vec{B})}{\Vert\left(\mathbf{\vec{R}_{\mathbf{V}}\left(P\right)}_{2,1}-\vec{B}\right)\times(\vec{A}-\vec{B})\Vert}+\vec{B}, \vec{B}\right) \\ \left(\frac{\left(\mathbf{\vec{R}_{\mathbf{V}}\left(P\right)}_{3,1}-\vec{A}\right)\times(\vec{B}-\vec{A})}{\Vert\left(\mathbf{\vec{R}_{\mathbf{V}}\left(P\right)}_{3,1}-\vec{A}\right)\times(\vec{B}-\vec{A})\Vert}+\vec{A}, \vec{A}\right) \\ \left(\frac{\left(\mathbf{\vec{R}_{\mathbf{V}}\left(P\right)}_{5,1}-\vec{B}\right)\times(\vec{C}-\vec{B})}{\Vert\left(\mathbf{\vec{R}_{\mathbf{V}}\left(P\right)}_{5,1}-\vec{B}\right)\times(\vec{C}-\vec{B})\Vert}+\vec{B}, \vec{B}\right) \\ \left(\frac{\left(\mathbf{\vec{R}_{\mathbf{V}}\left(P\right)}_{6,1}-\vec{A}\right)\times(\vec{C}-\vec{A})}{\Vert\left(\mathbf{\vec{R}_{\mathbf{V}}\left(P\right)}_{6,1}-\vec{A}\right)\times(\vec{C}-\vec{A})\Vert}+\vec{A}, \vec{A}\right) \end{bmatrix}; $$

Project $\vec{BD}$ onto the reference plane for any $i \in [1,6]$ at $R\left(i\right)$:

$$ \mathtt{\text{Let }}R\left(i\right)=\begin{Bmatrix} \vec{D}_r=\vec{F}\left(\vec{D},i,\mathbf{\vec{R}_{\mathbf{V}}\left(P\right)}_{i,j}\right), \\ \vec{B}_r=\vec{F}\left(\vec{B},i,\mathbf{\vec{R}_{\mathbf{V}}\left(P\right)}_{i,j}\right), \\ \vec{A}_r=\vec{F}\left(\vec{A},i,\mathbf{\vec{R}_{\mathbf{V}}\left(P\right)}_{i,j}\right), \\ \vec{BD}_r=\vec{D}_r-\vec{B}_r, \\ \vec{AB}_r=\vec{B}_r-\vec{A}_r \end{Bmatrix}; $$

Project $\vec{BD}$ onto the orthogonal plane for any $i \in [1,4]$ at $O\left(i\right)$:

$$ \mathtt{\text{Let }}O\left(i\right)=\begin{Bmatrix} \vec{D}_{o}=\vec{F}\left(\vec{D},i,\mathbf{\vec{O}_{\mathbf{V}}\left(P\right)}_{i,j}\right), \\ \vec{B}_{o}=\vec{F}\left(\vec{B},i,\mathbf{\vec{O}_{\mathbf{V}}\left(P\right)}_{i,j}\right), \\ \vec{A}_{o}=\vec{F}\left(\vec{A},i,\mathbf{\vec{O}_{\mathbf{V}}\left(P\right)}_{i,j}\right), \\ \vec{BD}_{o}=\vec{D}_{o}-\vec{B}_{o}, \\ \vec{AB}_{o}=\vec{B}_{o}-\vec{A}_{o} \end{Bmatrix}; $$

The angle between the projection of $\vec{AB}$ and $\vec{BD}$.

while projected onto the orthogonal plane: $\theta_{A_{o},D_{o}}=\arccos⁡\left(\frac{\vec{AB}_{o}\cdot\vec{BD}_{o}}{\Vert\vec{AB}_{o}\Vert\Vert\vec{BD}_{o}\Vert}\right)\implies\theta_{a_{o},d_{o}}= \arccos⁡\left(\frac{\left(\vec{B}_{o}−\vec{A}_{o}\right)\cdot\left(\vec{D}_{o}−\vec{B}_{o}\right)}{\Vert\vec{B}_{o}-\vec{A}_{o}\Vert\Vert\vec{D}_{o}−\vec{B}_{o}\Vert}\right);$

while projected onto the reference plane: $ \theta_{A_{r},D_{r}}=\arccos⁡\left(\frac{\vec{AB}_{r}\cdot\vec{BD}_{r}}{\Vert\vec{AB}_{r}\Vert\Vert\vec{BD}_{r}\Vert}\right)\implies\theta_{a_{r},d_{r}}= \arccos⁡\left(\frac{\left(\vec{B}_{r}−\vec{A}_{r}\right)\cdot\left(\vec{D}_{r}−\vec{B}_{r}\right)}{\Vert\vec{B}_{r}-\vec{A}_{r}\Vert\Vert\vec{D}_{r}−\vec{B}_{r}\Vert}\right); $