In general, a definition like $*3.01$ [in modern notation : $p \land q := \lnot (\lnot p \lor \lnot q)$] must be understood as an abbreviation.
I.e., we can replace in every context where we have used $p \land q$ the original formula without "altering" the set of theorems derivable.
Theoretically, it is unnecessary ever to give a definition ... the definitions are no part of our subject, but are, strictly speaking, mere typographical conveniences. Practically, of course, if we introduced no definitions, our formulae would very soon become so lengthy as to be unmanageable; but theoretically, all definitions are superfluous. (Chapter 1. Page 12, Merchant Books, 1910)
The usefulness of definition arises from two causes:
First, a definition usually implies that the definiens is worthy of careful consideration. Hence the collection of definitions embodies our choice of subjects and our judgment as to what is most important.
Secondly, when what is defined is (as often occurs) something already familar, such as cardinal or ordinal numbers, the definition contains an analysis of a common idea, and may therefore express a notable advance. (Chapter 1. Page 12, Merchant Books, 1910)
In $*4.5$ they merely reformulate the above definition as an equivalence. The comment is :
The following formulae are due to De Morgan [...]. The first
of them, it will be observed, merely embodies our definition of the logical
product.
The context of $*4.5$ is :
we shall be concerned with rules analogous, more or less, to those of ordinary algebra. It is from these rules that the usual "calculus of formal logic " starts. [...] Thus two
propositions are equivalent when they have the same truth-value.
The fundamental difference between *3.01 and *4.5 is that the latter asserts a proposition and the former does not assert any proposition. A definition does not always lead to the equivalence between the definiendum and the definien. Take *30.01 and *30.22 for example:
*30.01 $ R‘y =(℩x)(xRy) $ Df
*30.22 $ E!R‘y.≡.R‘y =(℩x)(xRy) $
Note that we do not necessarily have $R‘y =(℩x)(xRy)$ which is only true when $E!R‘y$.
This is because when an incomplete symbol appears in a proposition, the definiendum is the proposition, instead of the incomplete symbol in isolation. Thus, "the present King of France is the present King of France" is false. See *14.28 for further illustration.
There does not appear to be a general condition in PM that enables a definition to imply an equivalence. Such implications have to be proved in particular cases. This is why *3.01 cannot take the place of *4.5.
 https://i.stack.imgur.com/5Ujin.png
https://i.stack.imgur.com/5Ujin.png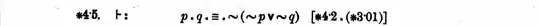 https://i.stack.imgur.com/ZQboI.png
https://i.stack.imgur.com/ZQboI.png