Chain Rule Intuition

Question

We know that the chain rule is used to differentiate a composite function ,say $$f(x) = h(g(x))$$ It's defined as the derivative of the outside function times the derivative of the inner function or the other way around.

$$\frac{\mathrm{dy} }{\mathrm{d} x} = \frac{\mathrm{dy} }{\mathrm{d} u} \cdot \frac{\mathrm{du} }{\mathrm{d} x}$$

Despite we know that the above expression is not a fraction (even though it's a fractional notation of the derivative used by Leibnitz) you can "cancel" the two du's and get back dy/dx.

My question is: How can you even think of cancelling du from dy/du and du from du/dx when they are not even fractions. Just because it's been multiplied do they automatically become fractions?Are they really being "multiplied"?

I'am really looking for an intuition behind this.To me this is some kind of fantasy.It doesn't appear to be real.

Answer 1

In a race, Usain Bolt is travelling twice as fast as a train which is going 3 times as fast as a horse. How much faster is Usain Bolt travelling than the horse?

$$ \frac{d\text{Bolt}}{d\text{Horse}}= \frac{d\text{Bolt}}{d\text{Train}} \cdot \frac{d\text{Train}}{d\text{Horse}} = 2\cdot 3 = 6 $$

Answer 2

If $h$ and $g$ are linear functions, then it should be obvious what the chain rule must hold. The general chain rule is simply this observation plus the fact that derivatives provide good linear approximations.

Answer 3

Here's the intuition I give every time I teach the Chain Rule:

Remember that derivatives are rates, the Chain Rule explains how to meaningfully multiply these rates together. A cheetah is 4 times as fast as a man, and a man is 10 times as fast as a snail. You can see right away how to compare the cheetah to the snail-- the cheetah is 40 (that is, 4x10) times as fast.

The Chain Rule is just the formula for computing more difficult derivatives by using an intermediate step. We have $y=f(x)$, and we can get the rate of change of $y$ with respect to $x$ by going through an intermediate variable $u=g(x)$ (where $f(x)=h(g(x))$). We get $$f'(x)= h'(g(x)) \, g'(x)$$ or, equivalently, $$ \frac{dy}{dx} = \frac{dy}{du} \frac{du}{dx}.$$

---

The above is just a quick intuitive explanation for why the Chain Rule involves multiplying derivatives and "canceling." Rahul's answer explains a proof for this fact.

Having proofs is essential, because sometimes derivatives may not work as you expect. For example, if you have $z=f(x,y)$ where $x$ and $y$ are both functions of $t$, the Chain Rule looks like $$\frac{dz}{dt} = \frac{\partial z}{\partial x} \frac{dx}{dt} + \frac{\partial z}{\partial y} \frac{dy}{dt},$$ which is not the same as ordinary fraction cancelling.

Answer 4

$$ \frac{dy}{dx} = \lim_{\Delta x\to 0}\frac{\Delta y}{\Delta x} = \lim_{\Delta x\to0} \frac{\Delta y}{\Delta u} \cdot\frac{\Delta u}{\Delta x}. $$ When you write that, then it's just cancellation.

(Ordinary "limit laws" will get you from there to $\left(\lim\limits_{\Delta x\to0}\dfrac{\Delta y}{\Delta u} \right)\cdot \left(\lim\limits_{\Delta x\to0} \dfrac{\Delta u}{\Delta x}\right)$, but notice that the first limit here says $\text{“}\Delta x\to 0\text{,''}$ not $\text{“}\Delta u \to0.\text{''}$ That you can put $\Delta u$ there depends on the fact that differentiable functions are continuous. Then there's a moderately hairy difficulty of what to do when $\Delta u=0$ and $\Delta x\ne 0$.)

Answer 5

By creating a system where f(x) and g(x) are orthogonal to each other the derivation for the chain rule becomes very transparent. Please see image above.

Answer 6

Others have already answered the question directly and provided good intuition for why the chain rule works, so I will just add a graphical interpretation of the chain rule in the form $[f(g(x))]'=f'(g(x))g'(x)$.

By far the best explanation of this form I've seen is found here, but I will summarize the answer in case the link ever becomes broken.

Consider two functions, $f(x)=x^2$ and $f(2x)=(2x)^2$:

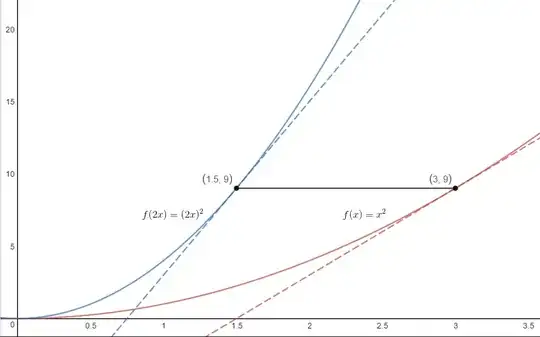
Notice that the range of both functions stays the same, since only the rate of input is being modified. Also notice that $f(2x)$ is "scrunched", since it is cycling through its input twice as fast.

Now, consider the tangent lines to the graph at the two points marked in the picture. Although the outputs of the function are the same ($f(2*1.5) = f(3)$), the slope of $f(2x)$ at $(1.5,9)$ is steeper than the corresponding slope at $(3,9)$ (in fact, twice as steep). The reason for this, in the words of the aforementioned article, is that slope is "rise over run", and you have half as much "run" on $f(2x)$ than you do for the equivalent point on $f(x)$. (By "equivalent", I mean points such as $(1.5, 9)$ and $(3,9)$ for two functions $f(g(x))$ and $f(x)$, respectively.)

Relating this back to the formula $[f(g(x))]'=f'(g(x))g'(x)$, we have $f(x)=x^2$ and $g(x)=2x$. If we want to calculate the slope at $x=1.5$ for $f(2x)$, what this formula is saying is "take the ORIGINAL slope at $(3,9)=(1.5, f(2*1.5))$, and scale it by how fast $g(x)$ is changing." Since $g(x)$ is changing twice as fast as the input to $f$ normally changes without composition, you will have exactly $\frac{1}{g'(x)}=\frac{1}{2}$ as much "run" in your slope at $(1.5,9)$ compared to $(3,9)$, and thus you need to scale the original slope at $(3,9)$ by $g'(x)=2$ in this example.

In general, if you have a composite function in the form of $f(g(x))$, the input to $f$ is changing $g'(x)$ as fast the input normally changes without composition, and thus you need to scale the slope at $f(g(x))$ by exactly $g'(x)$.

Answer 7

Think of the plot of $f(x)$ and $f(3x)$. It is clear that the slope in the second case is 3 times as large. Now, change the factor at each point...

Answer 8

If you look at $f$ as a function of $g$, then you'd get that the differential of $f$ is $df=f'(g)dg$.

Now do the same thing for $g$ by considering that is is a function of $x$: $dg=g'(x)dx$.

Hence $df=f'(g)dg=f'(g(x))g'(x)dx$, or, $\frac{df}{dx}=f'(g(x))=f'(g(x))g'(x)$.

This is what we are doing when using a u-sub in integration: $$\int f'(g(x))g'(x)dx=\int f'(g)dg$$