2

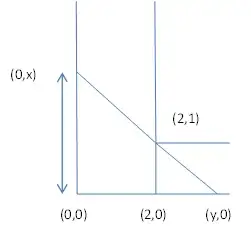
enter image description here

The question:

I'm given the figure shown above, and need to calculate the length of the longest rod that can fit inside this figure and rotate the corner.

My thoughts: I have tried doing the following : put $(0,0)$ at the bottom left corner. This way, the place where the rod touches the upper block is $(2,1) $ , and if we denote by $(2+t,0)$ the place where the rod touches the lower block, we get that the place where it touches the lower block is $y=t+2 $ , and then, the length is $d=\sqrt{2}(t+2)$ which doesn't have a maximum.

What am I doing wrong ?

THe final answer should be $ \sqrt{(1+\sqrt[3]{4} ) ^2 + (2+\sqrt[3]{2})^2 } $ .

Thanks !

MJD
  • 65,394
  • 39
  • 298
  • 580
criticism
  • 127
  • Sorry, this is no help. But this problem is somehow related to the hard "moving sofa" problem, so I thought I provide a link: http://math.stackexchange.com/questions/533436/why-are-these-geometric-problems-so-hard – B0rk4 Dec 31 '13 at 01:20
  • 1
    See http://math.stackexchange.com/questions/583707/intuitive-explanation-for-formula-of-maximum-length-of-a-pipe-moving-around-a-co – Matthew Conroy Dec 31 '13 at 01:22
  • @criticism : +1 for the picture – Stefan Smith Dec 31 '13 at 02:03

4 Answers4

1

enter image description here

$y = 2+\frac{2}{x-1}$

$ L = \sqrt{x^2 + (2+\frac{2}{x-1})^2}$

Take the derivative of the function inside the square root and equate it to 0

$\frac{dL}{dx} = (x-1)^{3} - 4 = 0$

$x=4^{1/3} + 1$

Thus $L = \sqrt{(4^{1/3} + 1)^2 + (2+2^{1/3})^2}$

Satish Ramanathan
  • 11,984
0

Hm, your mistake is citing wrong question. You missed the most important condition: The rod CAN PASS through the that corner.

The answer for this problem should be like: i) We observe that: Denote A is a point on the left wall of block , B is a point on the lower wall of block and AB pass through the (2;1). Then point then if min(AB) >= length of rod then the rod may pass the cornet. ii) The rest is similar to your, denote the lower point is (2+t;0) .Second, find the upper point A .Finally, find the minimum value of AB.

user118358
  • 1
0

Your mistake is in the assertion that "the place where it touches the lower block is $y=t+2$." If you draw a picture and label the lengths of the sides of the appropriate right triangles, you'll see that in fact it touches the lower block at $y=1+{2\over t}$. This gives $(2+t)^2+(1+{2\over t})^2$ as the expression for the square of the length of the pipe. Differentiated appropriately, it has a minimum at $t=\sqrt[3]2$, and the rest should follow.

Barry Cipra
  • 79,832
0

Let's say the rod makes an angle $\theta$ with the long wall. Let's say the wide area has width $W$ and the narrow area has width $N$. Then, the length of the rod that can fit in at angle $\theta$ is

$$x = \frac{W}{\sin \theta} + \frac{N}{\cos \theta} = W \csc \theta + N \sec \theta.$$

There's a minimum in there at some $\theta$:

$$\frac{dx}{d \theta} = N \sec \theta \tan \theta - W \csc \theta \cot \theta = 0.$$

This simplifies to

$$\tan^3 \theta = W/N = 2.$$

Now if $\tan \theta = \sqrt[3]{2},$

$$\cos \theta = \frac{1}{\sqrt{1 + \sqrt[3]{4}}}; \sin \theta = \frac{\sqrt[3]{2}}{\sqrt{1 + \sqrt[3]{4}}},$$

and the rest should follow.

John
  • 26,319