Prove that $A + B = C$

Question

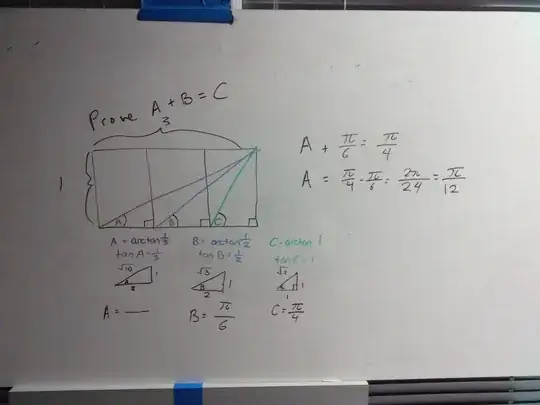
I drew the diagram here enter image description here

I honestly do not see how $A$ and $B$ could possibly equal $C$.

You've incorrectly determined $B.$ We know that $\sin\dfrac\pi6=\dfrac12,$ but $\tan\dfrac\pi6=\dfrac1{\sqrt3}.$ — Cameron Buie, Dec 27 '13 at 19:51
Tan(pi/6) != 1/2. Sin(pi/6) = 1/2. The hypotenuse is of length 2, not the bottom edge — John Dvorak, Dec 27 '13 at 19:52
Related : http://math.stackexchange.com/questions/138310/show-that-2-tan-12-pi-cos-1-frac35/583359#583359 — lab bhattacharjee, Dec 28 '13 at 07:53

score 2 · Answer 1 · answered Dec 27 '13 at 20:04

2

Hint: Observe that $0<A+B<\pi.$ What is $\tan(A+B)$? What is $\tan C$? Why is knowing these things enough?

answered Dec 27 '13 at 20:04

Cameron Buie

102,994

score 1 · Answer 2 · answered Dec 27 '13 at 23:34

$\sin A = \dfrac{1}{\sqrt{10}}$, $\cos A = \dfrac{3}{\sqrt{10}}$, $\sin B = \dfrac{1}{\sqrt5}$, $\cos B = \dfrac{2}{\sqrt5}$, $\sin C = \cos C = \dfrac1{\sqrt2}$.

$\sin(A + B)= \sin A \cos B + \cos A \sin B = \dfrac2{5\sqrt{2}} + \dfrac3{5\sqrt{2}} = \dfrac1{\sqrt{2}}= \sin C$

$\cos(A + B) = \cos A \cos B - \sin A \sin B = \dfrac6{5\sqrt{2}} - \dfrac1{5\sqrt{2}} = \dfrac1{\sqrt{2}} = \cos C$

Since their sines and cosines are equal, $C$ and $A + B$ are congruent modulo $2\pi$. Since also $ 0 \lt A \lt B \lt C \lt \dfrac\pi{2}$, $-\dfrac{\pi}2 \lt C - (A + B) \lt \dfrac{\pi}2$, $A + B$ and $C$ must be equal.

leonbloy · Accepted Answer · 2013-12-28T22:47:18.507

Without trigonometry:

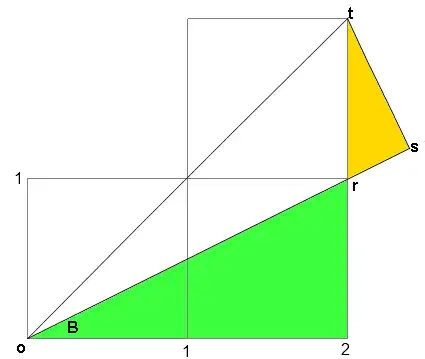
enter image description here

Green and yellow triangles are similar. Then, $\overline{s t}=2 \, \overline{r s}$ and $\overline{s t}^2+\overline{r s}^2=1$, therefore $\overline{r s}=\frac{1}{\sqrt{5}}$ and $\overline{s t}=\frac{2}{\sqrt{5}}$

Furthermore, $\overline{os}= \overline{r s}+ \sqrt{1^2+2^2}= \frac{6}{\sqrt{5}}$

Hence, $$\frac{\overline{o s}}{\overline{s t}} = 3$$

Then, identifying $\widehat{sot}=A$, we conclude that $B+A=C$

Prove that $A + B = C$

3 Answers3