33

I ran across this integral I get no where with. Can someone suggest a method of attack?.

$$\int_0^{\infty}\frac{\sin(\pi x^2)}{\sinh^2 (\pi x)}\mathrm dx=\frac{2-\sqrt{2}}{4}$$

I tried series, imaginary parts, and so forth, but have made no progress.

Thanks very much.

J. M. ain't a mathematician
  • 75,051
Cody
  • 14,054
  • 1
    If it's any consolation, Mathematica can't solve "Integrate[Sin[Pi*x^2]/Sinh[Pi*x]^2, {x,0,Infinity}]", which means it's not easy. –  Sep 03 '11 at 16:53
  • @barrycarter: Almost two years later, Mathematica still can't get this one. – robjohn Jul 30 '13 at 22:04
  • 4
    I love it when a brilliant human mind evaluates an integral the fancy math engines can not.:) – Cody Jul 31 '13 at 11:15
  • @robjohn $\texttt{Mathematica}$ claims that $\texttt{Log[...]}$ assumes a branch-cut along $\left(-\infty,0\right]$. However, it returns $\texttt{Log[-1]} = \pi,\mathrm{i}$ – Felix Marin Apr 06 '17 at 22:21
  • @robjohn $\texttt{Mathematica}$ is unable to evaluate ( at least version 10.0.0.0 ) the simple integral $$ \int_{-\infty}^{\infty}{g/\pi \over \left(\omega - \varepsilon\right)^2 + g^{2}}, {1 \over \mathrm{e}^{\omega/t} + 1},\mathrm{d}\omega = {1 \over 2} - {1 \over \pi},\Im\Psi\left({1 \over 2} + { g + \varepsilon,\mathrm{i}\over 2\pi t}\right),,\quad g > 0,,\ \varepsilon \in \mathbb{R},,\ t > 0 $$ – Felix Marin Apr 06 '17 at 23:37
  • This is equivalent to proving that $~\displaystyle\int_0^\infty\Big[\coth\big(\pi\sqrt x\big)-1\Big]~\cos\big(\pi x\big)~dx~=~\dfrac{2-\sqrt2}4.~$ – Lucian Sep 02 '17 at 17:28
  • Six years later, and Mathematica is still unable to solve this. Version 11.01 – Enrico M. Nov 10 '17 at 20:29
  • 1
    @Turing $22nov2020$: No yet. – Felix Marin Nov 22 '20 at 05:01
  • 1
    @FelixMarin This is why I love the (human) brain! – Enrico M. Nov 22 '20 at 17:57

5 Answers5

23

It can be done using contour integration and the calculus of residues.

Sketch: Integrate $$ f(z) = \frac{e^{i\pi z^2} e^{\pi z}}{\sinh^2 (\pi z) \cosh(\pi z)} $$ around a rectangular contour with corners at $\pm R$ and $\pm R + i$ and with semicircular indentations of radius $\epsilon$ to avoid the poles at $0$ and $i$, take imaginary parts and let $R\to\infty$, $\epsilon\to 0^+$.

You'll need to use $$ f(x)-f(x+i)=\frac{2 e^{i \pi x^2}}{\sinh^2(\pi x)} $$ together with $$ \operatorname*{res}_{z=0} \, f(z) = \operatorname*{res}_{z=i} \, f(z) = \frac{1}{\pi} $$ (since these will each contribute $-i \pi$ times the residue in the limit $\epsilon \to 0^+$) and $$ \operatorname*{res}_{z=i/2} \, f(z) = \frac{-1+i}{\pi\sqrt{2}}. $$

Hans Lundmark
  • 53,395
20

Although this question is two years old, the integral was mentioned in chat recently, I evaluated it, and then found this question. Since there is no complete solution, although Hans Lundmark's suggestion is excellent and similar in nature, I am posting what I have done.

Contours

Since the integrand is even, $$ \begin{align} \int_0^\infty\frac{\sin(\pi x^2)}{\sinh^2(\pi x)}\,\mathrm{d}x &=\frac12\int_{-\infty}^\infty\frac{\sin(\pi x^2)}{\sinh^2(\pi x)}\,\mathrm{d}x \end{align} $$ Define $$ f(z)=\frac{\cos\left(\pi z^2\right)}{\sinh(2\pi z)\sinh^2(\pi z)} $$ Note that because $$ f(x\pm i) =\frac{-\cos\left(\pi x^2\right)\cosh(2\pi x)\pm i\sin\left(\pi x^2\right)\sinh(2\pi x)}{\sinh(2\pi x)\sinh^2(\pi x)}\\ $$ we have $$ \begin{align} \int_\gamma f(z)\,\mathrm{d}z &=\int_{-\infty}^\infty\big[f(x-i)-f(x+i)\big]\,\mathrm{d}x\\ &=-2i\int_{-\infty}^\infty\frac{\sin(\pi x^2)}{\sinh^2(\pi x)}\,\mathrm{d}x\\ &=2\pi i\times\begin{array}{}\text{the sum of the residues}\\\text{inside the contour}\end{array} \end{align} $$ where $\gamma$ is the contour

$\hspace{3.2cm}$enter image description here

Therefore, $$ \int_0^\infty\frac{\sin(\pi x^2)}{\sinh^2(\pi x)}\,\mathrm{d}x =-\frac\pi2\times\begin{array}{}\text{the sum of the residues}\\\text{inside the contour}\end{array} $$ Residues

near $0$ : $$ \begin{align} f(z) &=\frac{\cos\left(\pi z^2\right)}{\sinh(2\pi z)\sinh^2(\pi z)}\\ &=\frac{1-\frac12\pi^2z^4+O(z^8)}{2\pi z\left(1+\frac23\pi^2z^2+O(z^4)\right)\pi^2 z^2\left(1+\frac13\pi^2z^2+O(z^4)\right)}\\ &=\frac{1-\pi^2z^2}{2\pi^3z^3}+O(z)\\[10pt] &\implies\text{residue}=-\frac1{2\pi} \end{align} $$ at $\pm i/2$, use L'Hosptal : $$ \begin{align} \text{residue} &=\lim_{z\to\pm i/2}\frac{(z\mp i/2)\cos\left(\pi z^2\right)}{\sinh(2\pi z)\sinh^2(\pi z)}\\ &=\frac1{2\pi\cosh(\pm\pi i)}\frac{\cos(-\pi/4)}{\sinh^2(\pm\pi i/2)}\\ &=\frac1{2\pi\cos(\pm\pi)}\frac{\sqrt2/2}{-\sin^2(\pm\pi/2)}\\[4pt] &=\frac{\sqrt2}{4\pi} \end{align} $$ near $\pm i$ : $$ \begin{align} f(z\pm i) &=\frac{-\cos\left(\pi z^2\right)\cosh(2\pi z)\pm i\sin\left(\pi z^2\right)\sinh(2\pi z)}{\sinh(2\pi z)\sinh^2(\pi z)}\\ &=\frac{-\left(1-\frac12\pi^2z^4+O(z^8)\right)\left(1+2\pi^2z^2+O(z^4)\right)+O(z^3)}{2\pi z\left(1+\frac23\pi^2z^2+O(z^4)\right)\pi^2 z^2\left(1+\frac13\pi^2z^2+O(z^4)\right)}\\ &=-\frac{1+\pi^2z^2}{2\pi^3z^3}+O(1)\\[10pt] &\implies\text{residue}=-\frac1{2\pi} \end{align} $$ Result

Thus, $$ \begin{align} \int_0^\infty\frac{\sin(\pi x^2)}{\sinh^2(\pi x)}\,\mathrm{d}x &=-\frac\pi2\left(-\frac1{2\pi}-\frac1{2\pi}+\frac{\sqrt2}{4\pi}+\frac{\sqrt2}{4\pi}\right)\\[6pt] &=\frac{2-\sqrt2}{4} \end{align} $$

robjohn
  • 345,667
  • Wow, that's nice robjohn. It sure doesn't bother me that it is two years old. I always enjoy seeing your clever solutions. I can give an upvote. I hate to take Hand greenie away :) – Cody Jul 30 '13 at 21:17
  • No, I wouldn't want to do that. Now, I may change my mind if I find a real-only solution :-) – robjohn Jul 30 '13 at 22:02
  • I like your residue method. It is a stroke of genius how you found that function to consider. I sure would not have thought of that. Upon finding the correct f(z) to consider, a lot of these contour integrals become rather straightforward. If I get lucky and find a real solution, I will certainly post it. – Cody Jul 31 '13 at 11:08
  • If I can find the proper inverse Laplace transform, this answer should prove useful. However, it looks as if the inverse Laplace transform might be equivalent to this problem. – robjohn Jul 31 '13 at 11:59
  • Actually, finding the proper $f$ was just a bit of experimentation. First, I looked at $$ \frac{\sin(\pi(x\pm i)^2)}{\sinh^2(\pi(x\pm i))}=\frac{-\sin(\pi x^2)\cosh(2\pi x)\mp i\cos(\pi x^2)\sinh(2\pi x)}{\sinh^2(\pi x)} $$ I noticed that subtracting one from the other left $2i\cos(\pi x^2)\sinh(2\pi x)$ in the numerator. So I tried $$ \frac{\cos(\pi(x\pm i)^2)}{\sinh^2(\pi(x\pm i))}=\frac{-\cos(\pi x^2)\cosh(2\pi x)\pm i\sin(\pi x^2)\sinh(2\pi x)}{\sinh^2(\pi x)} $$ – robjohn Jul 31 '13 at 12:19
  • which left $-2i\sin(\pi x^2)\sinh(2\pi x)$ in the numerator after subtraction. The $\sinh(2\pi x)$ is easy to get rid of: since $\sinh(2\pi(x\pm i))=\sinh(2\pi x)$, we can just divide it out. Thus, $$ \frac{\cos(\pi(x\pm i)^2)}{\sinh^2(\pi(x\pm i))\sinh(2\pi(x\pm i))}=\frac{-\cos(\pi x^2)\coth(2\pi x)\pm i\sin(\pi x^2)}{\sinh^2(\pi x)} $$ Therefore, we want to use $$ f(z)=\frac{\cos(\pi z^2)}{\sinh^2(\pi z)\sinh(2\pi z)} $$ – robjohn Jul 31 '13 at 12:19
  • That's clever how you came up with it. Thanks for the thorough explanation. – Cody Aug 01 '13 at 10:49
  • Actually there seems to be a an issue with Hans Lundmark's evaluation. In the limit, the indentations at $0$ and $i$ (both of which are poles of order 2) don't contribute $- \pi i$ times the residue. They blow up. But amazingly you arrive at the correct answer if you assume they do. – Random Variable Aug 02 '13 at 06:03
  • @RandomVariable: if we look at the imaginary part of the functions in Hans Lundmark's answer, things look less explosive. – robjohn Aug 02 '13 at 10:08
  • Plugging in small values for $\epsilon$, the imaginary part of $ \displaystyle \lim_{\epsilon \to 0} \int_{\pi}^{0}\frac{e^{i \pi(\epsilon^{2}e^{2it})}e^{\pi \epsilon e^{it}}}{\sinh^{2} (\pi \epsilon e^{it}) \cosh(\pi \epsilon e^{it})} i \epsilon e^{it} \ dt$ does appear to be finite and approaching $-1$, that is, $-i \pi \text{Res}[f,0]$. It seems daunting to separate the integrand into it's real and imaginary parts. But I guess I could replace $\sinh^{2}(\pi \epsilon e^{it})$ with $\pi^{2} \epsilon^{2} e^{2it}$. Am I approaching this correctly? – Random Variable Aug 02 '13 at 15:15
  • @RandomVariable: Why would you want to replace $\sinh^2(\pi\epsilon e^{it})$ with $\pi^2\epsilon^2e^{2it}$? – robjohn Aug 02 '13 at 17:11
  • 3
    While it is true that $\sinh(z)\approx z$, one has to be careful since $\frac1{z^3}$ has a residue of $0$ at $z=0$, but $\frac1{\sinh^3(z)}$ has a residue of $-\frac12$ at $z=0$. Rather than looking at $\epsilon e^{it}$, look at the power series near the singularity; e.g. near $0$, $$ \begin{align} \frac{e^{i\pi z^2}e^{\pi z}}{\sinh^2(\pi z)\cosh(\pi z)} &=\frac{\left(1+O\left(z^2\right)\right) \left(1+\pi z+O\left(z^2\right)\right)}{\pi^2z^2\left(1+O\left(z^2\right)\right) \left(1+O\left(z^2\right)\right)}\ &=\frac1{\pi^2z^2}+\frac1{\pi z}+O(1) \end{align} $$ – robjohn Aug 02 '13 at 18:49
  • 1
    Thus, that function has a residue of $\frac1\pi$ at $z=0$. If the contour looks similar to mine, but encompasses $0$ and misses $i$, then we only need worry about the sum of the residues at $0$ and $i/2$. However, you are right, and he shouldn't be considering half the residue at points where the singularity is greater than degree 1. – robjohn Aug 02 '13 at 18:51
  • If you look at the Laurent series I give above, you see that as $\epsilon\to0$, we can ignore the $O(1)$ part and concentrate on the $\frac1{\pi^2z^2}+\frac1{\pi z}$ part. Your limit becomes – robjohn Aug 02 '13 at 20:11
  • 2
    $$ \begin{align} &\lim_{\epsilon\to0}\mathrm{Im}\int_\pi^0\left(\color{#C00000} {\frac1{\pi^2\epsilon^2} e^{-2it}}\color{#00A000} {+\frac1{\pi\epsilon} e^{-it}}\right)\epsilon ie^{it},\mathrm{d}t\ =&\lim_{\epsilon\to0}\mathrm{Im}\int_\pi^0\left(\color{#C00000} {\frac1{\pi^2\epsilon} e^{-it}}\color{#00A000} {+\frac1{\pi}}\right)i,\mathrm{d}t\ =&\lim_{\epsilon\to0}\mathrm{Im}\left(\color{#C00000}{\frac{-2}{\pi^2\epsilon}} \color{#00A000}{-i}\right)\ =&\color{#C00000}{0}\color{#00A000}{-i} \end{align} $$ – robjohn Aug 02 '13 at 20:11
  • @RandomVariable: Oops. you're right (fixed). Actually, I had first given the Laurent expansion to find the residue. In my answer, I just count the residues inside the contour, and rely on the cancellation in $f(x-i)-f(x+i)$ and the fact that my contours are exactly $2i$ apart. However, since you were interested in the limit along the infinitesimal semi-circle, I used it there, too. :-) – robjohn Aug 02 '13 at 21:42
  • In my answer, we have $$ f(x-i)-f(x+i)=-2i\frac{\sin(\pi x^2)}{\sinh^2(\pi x)} $$ and that is bounded near $0$. Thus, integrating along contour shown cancels nicely even on the semi-circles. – robjohn Aug 03 '13 at 00:09
  • @RandomVariable: my argument only relies on which singularities are inside the contour and that the upper and lower parts of the contour are separated by $2i$. They don't even really need semi-circular indentations, just that their average approaches the real axis. – robjohn Aug 03 '13 at 21:40
  • I just noticed this problem on that German site with no solution. http://de.wikibooks.org/wiki/Formelsammlung_Mathematik:_Bestimmte_Integrale:_Form_R%28x,sin,sinh%29 Perhaps that is where I had initially saw it. I do not remember. The one just below it appears to be a general form that looks to have some of the ideas outlined by robjohn and Hans – Cody Aug 03 '13 at 22:51
  • @RandomVariable: which argument is that? The theory of residues is all about the sum of the residues inside a contour. We can only use the semi-circles when the the singularity has degree $1$. Any higher, and the integral blows up as the radius of the semi-circle goes to $0$. – robjohn Aug 04 '13 at 00:29
  • In most situations that's true. But it's not true when it comes to specifically semi-circles and functions whose Laurent expansions at $z_{0}$ have no terms of the form $ \displaystyle\frac{1}{z^{2n}}$. In this situation the contribution from a negatively-oriented semi-circle indention at $z_{0}$ will be $- i \pi \text{Res} [f,z_{0}]$. – Random Variable Aug 04 '13 at 01:17
  • I should have said no terms of the form $ \displaystyle\frac{1}{(z-z_{0})^{2n}}$. And $n$ is meant to be a positive integer. – Random Variable Aug 04 '13 at 02:53
1

Not sure if anyone is interested in another solution after all those years, but anyway: I managed to evaluate the integral in a slightly different manner that doesn't depend on me coming up with a cleverly constructed function to integrate. However, cleverness is needed elsewhere in the process, so it's not much simpler than the other two solutions.

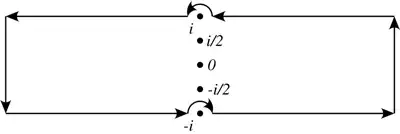
Define $\displaystyle f(z) = \frac{\mathrm{e}^{\mathrm{i}\pi z^2}}{\sinh^2 \pi z}$ and consider the two contours shown on the following sketch:

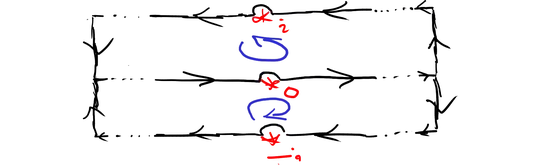
enter image description here

$f(z)$ has poles in all $\mathrm{i}n$ for $n \in \mathbb Z$; some of them are shown with red asterisks. Here the two rectangles extend to $\pm\infty$ on the sides, the little circles around the poles have radius $r > 0$ and the three horizontal lines are exactly the same, just shifted by $\pm \mathrm{i}$.

The residue of $f(z)$ in zero is obviously zero, because the Laurent series will contain only even powers. To calculate the residue in $z = \mathrm i$, write $w = z-\mathrm i$ and consider the fact that $\sinh^2 z$ is $\mathrm{i}$-periodic to obtain

$$ \frac{\mathrm{e}^{\mathrm{i} \pi (w^2 + 2\mathrm{i} w - 1)}}{\sinh^2 \pi w} = - \frac{1}{\pi^2 w^2} \frac{\mathrm{e}^{\mathrm{i} \pi w^2}}{(1 + \text{even powers of $w$})^2} (1 - 2\pi w + \cdots)$$

The only way to get the minus first power is to take the $-2\pi w$ in the last parentheses and 1's in the expansions of the other two functions. Hence the residue is $2/\pi$.

Now denote $\displaystyle I = \int_K f(x)\,\mathrm{d} x$, where $K$ is the horizontal line with a little circle around 0. Writing the residue theorem for the top and the bottom contour on the sketch, we get

$$\begin{align*} \int_K f(x)\,\mathrm{d} x - \int_K f(x+\mathrm{i})\,\mathrm{d} x &= 2\pi\mathrm{i} \times \frac{2}{\pi} &\implies&& \int_K \frac{\mathrm{e}^{\mathrm{i} \pi x^2} \mathrm{e}^{-2\pi x}}{\sinh^2 \pi x}\,\mathrm{d} x &= 4\mathrm{i} - I \\ \int_K f(x)\,\mathrm{d} x - \int_K f(x-\mathrm{i})\,\mathrm{d} x &= 0 &\implies&& \int_K \frac{\mathrm{e}^{\mathrm{i} \pi x^2} \mathrm{e}^{2\pi x}}{\sinh^2 \pi x}\,\mathrm{d} x &= - I \\ \end{align*}$$

Add the two equations together and subtract $\displaystyle 2 \int_K \frac{\mathrm{e}^{\mathrm{i}\pi x^2}}{\sinh^2 \pi x}\,\mathrm{d} x = 2I$ to get $$ \int_K \frac{\mathrm{e}^{\mathrm{i} \pi x^2} (\mathrm{e}^{2\pi x} - 2 + \mathrm{e}^{-2\pi x})}{\sinh^2 \pi x}\,\mathrm{d} x = 4\mathrm{i} - 4I. $$ However, $\sinh^2 \pi x = \frac14 (\mathrm{e}^{\pi x} - \mathrm{e}^{-\pi x})^2$, so the parenthesis in the numerator is $4\sinh^2 \pi x$. The sinh's cancel and we get $4 \int_K \mathrm{e}^{\mathrm{i} \pi x^2}\,\mathrm{d} x = 4\mathrm{i} - 4I$.

Taking the imaginary part of the last equality, sending $r \to 0$ to get rid of the small circle around the pole in $0$ (we couldn't do this earlier because the real part of the integral over the little circle actually diverges; however, the residue is 0, so, once we get rid of the divergence, there will be no contribution) and dividing by 8, we get $$ \frac12 \int_{-\infty}^\infty \sin \pi x^2\,\mathrm{d} x = \frac12 - \frac12 \int_{-\infty}^\infty \frac{\sin \pi x^2}{\sinh^2 \pi x}\,\mathrm{d} x. $$ Both integrands are even, so we can write $\int_{-\infty}^\infty = 2 \int_0^\infty$. The integral on the left is one of the well-known Fresnel integrals and it is equal to $\frac{1}{2\sqrt2}$, so we truly obtain the result

$$\int_0^\infty \frac{\sin \pi x^2}{\sinh^2 \pi x}\,\mathrm{d}{x} = \frac12 - \frac{1}{2\sqrt2} = \frac{2-\sqrt2}{4}.$$

Ramillies
  • 948
1

I would write the $\sin(x^2)$ as $(e^{ix^2}-e^{-ix^2})/2i$ and the sinh as $(e^{ x}-e^{-x})/2$. Then I'd maybe put the integrand in the form of $(e^{p_1(x)}+e^{p_2(x)}+\cdots)^{-1}+(e^{p_3(x)}+e^{p_4(x)}+\cdots)^{-1}+\cdots$ where $p_i(x)$ are polynomes with complex coefficients. I have no clue if that helps, to be honest.

Another idea would be partial integration after multiplying with 1, like: $\int\mathrm dx 1\cdot f(x)= xf(x)-\int\mathrm dx \; x\cdot f'(x)$ Sometimes this helps to handle a $x^2$ in the argument of a complicated function.

Michael Hardy
  • 1
Konstantin Schubert
  • 271
0

Numeric answer would be possible to get using the following tools:

  1. Riemann integration
  2. root-finding algorithm for the equation
  3. some limit sequence for the infinity giving better and better approximations

Riemann integration is needed to calculate F(x). Basically you'll need a root-finding algorithm that works with G : R->R functions, and gives a single x as solution. Just move the constant to the other side to get F(x)-F(0)-c=0. with G(x)=F(x)-F(0)-c. The infinity will break the riemann integration, so you'll need a sequence like { G(a_1)=0, G(a_2)=0, G(a_3)=0, ... } to get better and better approximations with a_1,a_2,a_3, ... sequence increasing towards infinity. The result then looks like {x_1, x_2,x_3,...} sequence which contains the values of x coming from root-finding algorithm.

But there could be better ways to solve this problem...

EDIT: there is problems with this solution. Namely, the a_i is a constant, not a variable, so root-finding might not be needed after all. All I get is approximation of 0=0.

tp1
  • 660