The following two exercises come from Logic for Mathematicians by J.B. Rosser, chapter 2 section one page 17. I am not so sure how to interpret the words "unless" and "except".
Notation: $\sim P$ represents negation the negation of $P$, and $PQ$ denotes $P\& Q$ which the author refers to as the logical product of $P$ and $Q$. Also, $P\equiv Q$ denotes "$P$ if and only if $Q$".
Exercise 3. If “$P$ ”, “$Q$ ”, and “$R$ ” are translations for “$x=y$ ” , “$x/z=y/z$ ”, and "$z\ne0$" , write a translation for “if $x=y$ , then $x/z=y/z$ except when $z=0$ ”
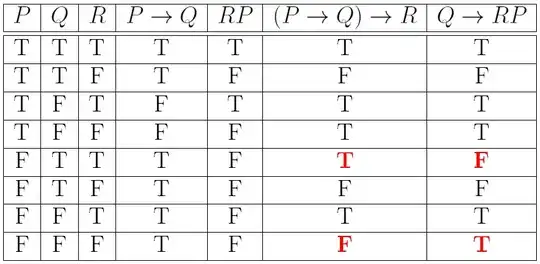
Solution: It is not the case that $(P\rightarrow Q)\sim R$ , i.e. we have $\sim[(P\rightarrow Q)\sim R]$ which is equivalent to $\sim[\sim(P\sim Q)\sim R]$ which is equivalent to $\sim\{[\sim P\sim(\sim Q)]\sim R\}$ (Note: the last step was an invalid manipulation, hence my conclusion is wrong) . Since $\sim(\sim Q)$ is equivalent to $Q$ and because the logical product is both associative and commutative, we have $\sim[Q\sim(PR)]$ hence $Q\rightarrow RP$.
My confusion is that I am pretty sure that $Q\equiv RP\space$ holds but i don't think that it would be the right translation. Am I right?
Exercise 4. If “$P$ ” and “$Q$ ” are the translations of “$(n-1)!+1$ is divisible by $n$ ” and “$n$ is prime” then write a translation for “$(n-1)!+1$ is not divisible by $n$ , unless $n$ is prime”
Solution: In other words we have that “the only time $(n-1)!+1$ is divisible by $n$ when $n$ is prime” or “$(n-1)!+1$ is divisible by $n$ when and only when $n$ is prime”, hence $P\equiv Q$.
I am not sure if I interpreted `unless' correctly here.
More Reasoning for Exercise 3:
I arrive at the conclusion $\sim[(P\rightarrow Q)\sim R]$ because it says "$P\rightarrow Q$ except when $\sim R$", which I take to mean that "it is false that both $\sim R$ and $P\rightarrow Q$ are true at the same time"; i.e. it is not the case that $(P\rightarrow Q)\&\sim R$, hence $\sim[(P\rightarrow Q)\sim R]$. From there mechanical manipulation of symbols gets me to $Q\rightarrow RP$ (again this is wrong).
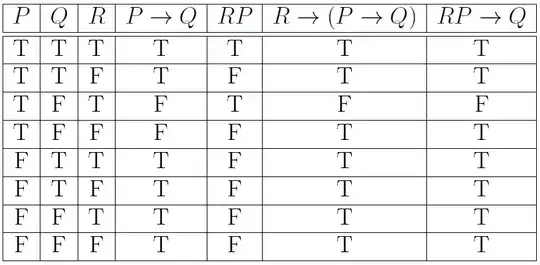
Additionally, though I am certain that $RP \rightarrow Q$ I am not quite sure how to reason this from the sentence “if $x=y$, then $x/z=y/z$ except when $z=0$”. Furthermore, with my interpretation of it being $\sim[(P\rightarrow Q)\sim R]$ I am not sure what symbolic manipulations would give $RP \rightarrow Q$.