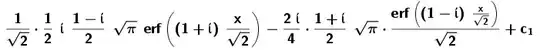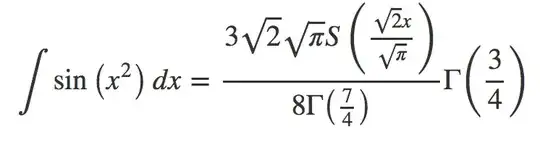$u$ substitution doesnt work. I don't see any connection with the Weierstrass substitution either. integration by parts results in a infinite integral series.
Asked
Active
Viewed 2,214 times
5
-
1take a look to the Fresnel Integrals – alexjo Dec 19 '13 at 15:53
-
is it possible to express this as a fourier series and than integrate that function? – adam Dec 19 '13 at 16:03
-
Fred Rickey has pointed out that the association of the substitution $u=\tan(x/2)$ with Weierstrass is a mistake. It goes back at least to Euler and no one seems to have found any evidence that Weierstrass ever mentioned it. I wonder if the error came only from Stewart's calculus books? – Michael Hardy Dec 19 '13 at 16:28
-
really now? That's something to ponder upon. I just read somewhere this is also a elliptical integral any explanation on that would be greatly appreciated – adam Dec 19 '13 at 19:26
3 Answers
8
this integral does not have a solution in terms of elementary functions. But, you can solve it using series methods. For instance, since
$$ \sin x = \sum \frac{(-1)^n x^{2n+1}}{(2n+1)!}$$
$$ \text{then} \; \; \sin (x^2) = \sum \frac{(-1)^n x^{4n+2}}{(2n+1)!}$$
$$ \int \sin (x^2) = \int \sum \frac{(-1)^n x^{4n+2}}{(2n+1)!} = \sum \frac{(-1)^n x^{4n+3}}{(2n+1)!(4n+3)} + K $$
ILoveMath
- 10,694
-
-
the well know functions from calculus: the trigonometric, exponentials, etc – ILoveMath Dec 19 '13 at 15:50
-
so there are some functions you cannot simply integrate? so how are you supposed to know before d oing so much work that it can't be done? there are nastier functions than this one but yet they turned out ti be integratable. – adam Dec 19 '13 at 15:55
-
2just experience will tell you. There is neither magic, nor mistery. Just Experience. – ILoveMath Dec 19 '13 at 16:03
-
It can also be proved, see differential Galois theory and this question on MSE or this one – Jean-Claude Arbaut Dec 19 '13 at 16:10
3
Mathematica returns:
$$\sqrt{\frac{\pi }{2}} S\left(\sqrt{\frac{2}{\pi }} x\right)$$
So, unless you consider Fresnel Sine to be an elementary function, that explains your troubles.
Igor Rivin
- 25,994
- 1
- 19
- 40
-
It is not a matter of whether or not you consider a function to be elementary. An elementary function is a well defined concept not subject to opinion. – Jon Claus Dec 19 '13 at 20:02
-
1@JonClaus Thanks for the terminological enlightenment! As you see from my profile, I am new to this math stuff... – Igor Rivin Dec 19 '13 at 20:27
1
By Geogebra, the result is:
But if you do it in python with below code:
import sympy as sym
from IPython.display import display
a = Integral(sin(x**2), x)
b = Eq(a,a.doit())
display(b)
The result is:
But I don't know how to understand the difference.
lucky1928
- 159