21

$$i^3=iii=\sqrt{-1}\sqrt{-1}\sqrt{-1}=\sqrt{(-1)(-1)(-1)}=\sqrt{-1}=i $$

Please take a look at the equation above. What am I doing wrong to understand $i^3 = i$, not $-i$?

Ian Mateus
  • 7,431
Rakanoth
  • 345
  • 41
    $\sqrt{a}\sqrt{b}=\sqrt{ab}$ is only guaranteed for positive reals. – robjohn Dec 18 '13 at 09:26
  • 4
    The third equal in your equation is not right. Please refer to http://en.wikipedia.org/wiki/Square_root#Notes – sebigu Dec 18 '13 at 09:26
  • 5
    The notation $\sqrt{a}$ is only well-defined (single-valued) for real, non-negative $a$ (unless you choose some principal value). Try to use $\pm\sqrt{a}$ much more than $\sqrt{a}$. It is still true that $\sqrt{a}\sqrt{b}=\pm\sqrt{ab}$ for complex numbers. – Jeppe Stig Nielsen Dec 18 '13 at 12:29
  • Isn't it simpler that that? i^3 is i * i * i. i * i = -1 -1 * i = -i Isn't that all there is to it? doug – Doug Lerner Dec 18 '13 at 12:16
  • 4
    There are so many duplicates of this : http://math.stackexchange.com/questions/3210/simple-complex-number-problem-1-1 http://math.stackexchange.com/questions/3210/simple-complex-number-problem-1-1 . Why dont you search before asking and what are the moderators doing , sigh ! – abkds Dec 18 '13 at 13:22
  • @Trafalgar Law, I am very very sorry for what I did :( I hope you forgive me. – Rakanoth Dec 18 '13 at 17:50
  • 3
    @TrafalgarLaw: more constructive, and friendly, might be to suggest how to search for this topic. Often knowing what to search for is not obvious. – robjohn Dec 19 '13 at 02:17

9 Answers9

56

Since $i^2=-1$ by definition, $i^3=i^2\cdot i=-i$.

$\sqrt{a}\sqrt{b}=\sqrt{ab}$ is only guaranteed for positive real $a$ and $b$.

robjohn
  • 345,667
51

We cannot say that $\sqrt{a}\sqrt{b}=\sqrt{ab}$ for negative $a$ and $b$. If this were true, then $1=\sqrt{1}=\sqrt{\left(-1\right)\cdot\left(-1\right)} = \sqrt{-1}\sqrt{-1}=i\cdot i=-1$. Since this is false, we have to say that $\sqrt{a}\sqrt{b}\neq\sqrt{ab}$ in general when we extend it to accept negative numbers.

Brian
  • 2,147
32

I'm sure everyone has answered the question appropriately. But here's my 2 cents:

From the Argand plane perspective, multiplying a complex number by $i$ is equivalent to rotating it about a circle (with radius = modulus of complex number) counterclockwise by 90 degrees. So ask yourself where you end up when you take $i$ and multiply it with $i$ twice.

Gautam Shenoy
  • 10,318
  • 3
    Yes. Many questions and confusions about complex numbers become simple and obvious when thinking about the geometric interpretation. – wim Dec 18 '13 at 11:40
13

$\sqrt{ab} = \sqrt{a} \sqrt{b}$ is correct in the following sense: In an arbitrary field (here it is the field of complex numbers) the root $\sqrt{a}$ is an element in some field extension such that $\sqrt{a}^2=a$. It is not uniquely determined, for if $b$ is a root, then also $-b$ is a root (and these only coincide when $a=0$ or the characteristic is $2$). Now the correct statement is:

  • If $\sqrt{a}$ and $\sqrt{b}$ are roots of $a$ resp. $b$, then $\sqrt{a}\sqrt{b}$ is a root of $ab$.

If we define $\sqrt{a}$ to be the set of all roots of $a$, then $\sqrt{ab}=\sqrt{a}\sqrt{b}$ even holds verbatim. For example, $\sqrt{-1}=\{\pm i\}$ then, and $\sqrt{(-1) (-1)} = \sqrt{-1} \sqrt{-1}$ holds since both sides equal $\{\pm 1\}$.

If $a \in \mathbb{R}^+$, one usually denotes by $\sqrt{a}$ the unique root of $a$ in $\mathbb{R}^+$, but this definition doesn't work properly for complex numbers or other fields.

Martin Brandenburg
  • 163,620
8

When you write $i=\sqrt{-1}$ then this is something that is sometimes useful and sensible, but really has to be done with care. All that really says is that $i^2=-1$, and of course $(-i)^2=-1$ holds as well. So correctly your calculation only yields $$(i^3)^2=i^2\cdot i^2\cdot i^2=(-1)(-1)(-1)=-1=i^2,$$ which is true.

Carsten S
  • 8,726
7

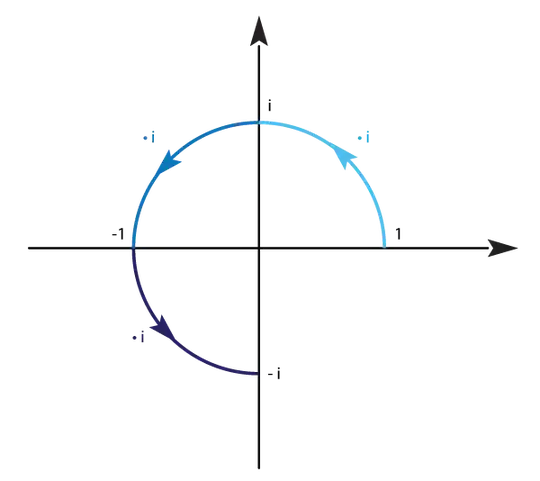
Multiplying by $i$ in the complex plane amounts to a counterclockwise turn of $90$ degrees. Hence it is geometrically clear that $i^3 = -i$, as the following drawing shows

enter image description here

Regarding your equations, as remarked already, $\sqrt{a}\sqrt{b}=\sqrt{ab}$ holds only for positive real $a$ and $b$, so you cannot use it with complex numbers.

Abramo
  • 6,917
4

$\sqrt[n]z$ does not return a single value, but n complex values. Hence your confusion, since both i and $-i$ are among the square roots of $-1$.

Lucian
  • 48,334
  • 2
  • 83
  • 154
2

Here is the Simple Answer to this question

as $i^2=-1$, if you break $i^3$ into $i^2\cdot i$ then you insert $-1$ into the place of $i^2$ you will get $(-1)\cdot i =-i$

this is the simple trick behind it.

Ian Mateus
  • 7,431
Husrat Mehmood
  • 121
-2

Someone posted earlier that it is i x i x i which is -1 x i, ie -i (but the post seems to have been deleted!

But that's all there is to it. It doesn't matter what i represents, the algebra will be consistent. But to prove it, substituting the value of i, ie (√-1), you get

√-1 x √-1 x √-1 = -1 x √-1 = -(√-1) = -i

However it may be worth mentioning that i is not a complex number as has been suggested - it is an irrational number. A complex number is of the form (x +iy)

haughtonomous
  • 11
  • 6
    $i$ is not an irrational number, it's an imaginary number. All real numbers and all imaginary numbers can also be considered complex numbers: they can be written as $x + 0 ⋅ i$ or $0 + y ⋅ i$. – hvd Dec 18 '13 at 12:57
  • $i=x+iy$ with $x=0$ and $y=1$. – Carsten S Dec 18 '13 at 17:22