Limit problem function

Question

Prove that the statement is wrong.

If $\lim f(x)$ exists but $\lim g(x)$ does not exist, then $\lim f(x)g(x)$ does not exist either.

score 4 · Answer 1 · answered Dec 16 '13 at 22:04

4

Consider $f(x) = \dfrac1x$, $g(x) = (-1)^{\lfloor x \rfloor}$. Consider $x \to \infty$ of $f(x)$, $g(x)$ and $f(x)g(x)$.

answered Dec 16 '13 at 22:04

2

And if Andi would like $g$ to be continuous, $g(x)=\sin x$ does nicely. – Brian M. Scott Dec 16 '13 at 22:11

score 4 · Answer 2 · answered Dec 16 '13 at 22:05

4

Consider $f(x) = 0$ and $g(x) = 1/x$, and look at the limits as $x \rightarrow 0$.

answered Dec 16 '13 at 22:05

John Hughes

93,729

score 1 · Answer 3 · answered Dec 16 '13 at 22:05

Consider the functions $$f(x) = 0 \quad \quad g(x) = x$$ and their infinite limits. Clearly $$\lim_{x \rightarrow \infty} f(x) = 0$$ Note that $\lim_{x \rightarrow \infty} g(x)$ does not exist. However, note $$f(x)g(x) = 0$$ Thus, $\lim_{n \rightarrow \infty} f(x)g(x) = 0$, which exists.

score 0 · Answer 4 · edited Apr 13 '17 at 12:21

0

Less trivial, as $\ x\to \infty,\ $ $\ 1/x \to 0\,$ and $\,\sin(x)$ doesn't exist, but $\ \sin(x)/x\to 0$

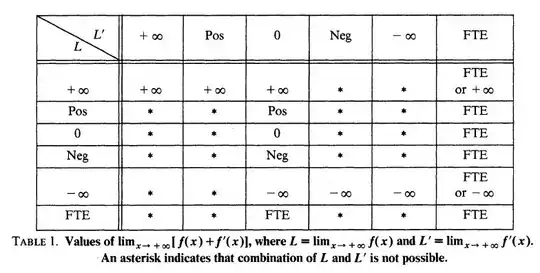
You may find it helpful to build tables of all possibilities for various types of limit problems. For example, see the table below, which arises from a slick solution to a classic old problem of Hardy (there you will find examples for all cases in the table).

L'Hospitable table

edited Apr 13 '17 at 12:21

Community

1

answered Dec 16 '13 at 22:53

Bill Dubuque

272,048

Limit problem function

4 Answers4