Prove $\sin^2\theta + \cos^2\theta = 1$

Question

How do you prove the following trigonometric identity: $$ \sin^2\theta+\cos^2\theta=1$$

I'm curious to know of the different ways of proving this depending on different characterizations of sine and cosine.

Answer 1

Let me contribute by this so let $$f(\theta)=\cos^2\theta+\sin^2\theta$$ then it's simple to see that $$f'(\theta)=0$$ then $$f(\theta)=f(0)=1$$

Answer 2

Since all methods are accepted, take the complex exponential defined as its series and consider the complex definitions of the trigonometric functions:

$$\cos (z)=\dfrac{e^{iz}+e^{-iz}}{2}\, \land \, \sin(z)=\dfrac{e^{iz}-e^{-iz}}{2i}, \text{ for all }z\in \mathbb C.$$

Take $\theta \in\mathbb R$. The following holds: $$\begin{align} (\cos(\theta))^2+(\sin (\theta))^2&= \dfrac{e^{ 2i\theta}+2+e^{-2i\theta}}{4}-\dfrac{e^{2i\theta}-2+e^{-2i\theta}}{4}\\ &=\dfrac {2-(-2)}4=1.\end{align}$$

Answer 3

Let $(\mathscr C)$ be a unit circle, and $\mathrm M\in(\mathscr C)$. Also, we will denote $\rm \angle{IOM}$ as $\theta$ (see the diagram). From the unit circle definition, the coordinates of the point $\rm M$ are $(\cos\theta,\sin\theta)$. And so, $\rm \overline{OC}$ is $\cos \theta$ and $\rm \overline{OS}$ is $\sin \theta$. Therefore, $\rm OM=\sqrt{\overline{OC}^2+\overline{OS}^2}=\sqrt{\cos^2\theta+\sin^2\theta}$. Since $\rm M$ lies in the unit circle, $\rm OM$ is the radius of that circle, and by definition, this radius is equal to $1$. It immediately follows that: $$\color{grey}{\boxed{\,\displaystyle\color{black}{\cos^2\theta+\sin^2\theta=1}}}$$

$\phantom{X}$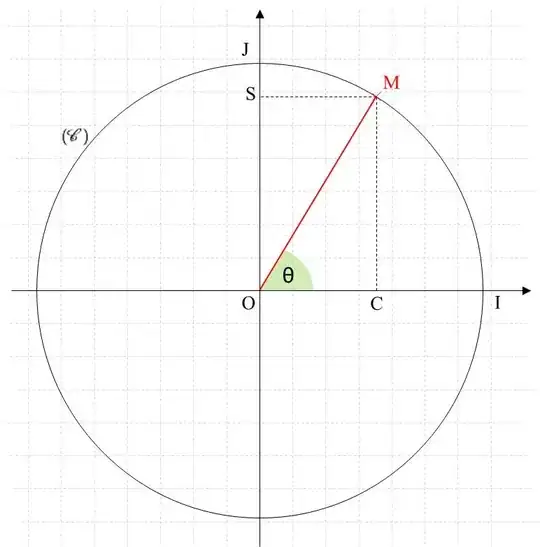

Answer 4

Consider a right-angled triangle, $\Delta ABC$, where $\angle BAC = \theta$,

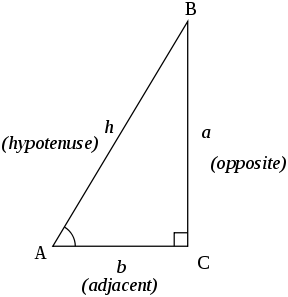
By the Pythagorean theorem, $$ {AC}^2+{BC}^2 = {AB}^2 $$ Dividing by $AB^2$, $$ \require{cancel} \begin{align} &\Rightarrow \frac{AC^2}{AB^2} + \frac{BC^2}{AB^2} = \frac{AB^2}{AB^2}\\ &\Rightarrow \Big(\frac{\text{opposite}}{\text{hypotenuse}}\Big)^2 + \Big(\frac{\text{adjacent}}{\text{hypotenuse}}\Big)^2 = \frac{\cancel{AB^2}}{\cancel{AB^2}} = 1\\ &\Rightarrow \boxed{\sin^2\theta + \cos^2\theta = 1} \end{align} $$

Answer 5

$$\large \sin^2\theta + \cos^2\theta =\sin\theta\sin\theta+\cos\theta\cos\theta =\cos(\theta-\theta) =\cos0 =1$$

Answer 6

If you choose to define sine and cosine by trigonometric rations, then JohnK's answer answers your question. There are other ways of answering your question that go with the different definitions of sine and cosine. Here are a few:

$(1)$, $\sin(x)$ is the solution to the differential equation $y''=-y$, $y(0)=0$, $y'(0)=1$, and $cos(x)$ is its derivative.

Proof of identity using $(1)$: $(\sin^2(x)+\cos^2(x))'=(y^2+y'^2)'= 2yy' + 2y'y''= 2yy'-2yy'=0$, now letting $x=0$ gives the identity. This is similar to Isaac's answer.

$(2)$, $\sin(x)= x-\frac{x^3}{3!} + \frac{x^5}{5!} - \ldots$ and $\cos(x)$ is its derivative.

Proof of identity using $(2)$: Define $e^{x}$ by its power series. Now show $e^{ix}=\cos(x)+i\sin(x)$, and use Git Gud's answer.

As you can see, these proofs are related, so its all a matter of definitions. I hope that helps :)

Answer 7

In the spirit of Git Gud's answer, differentiate $\sin^2 \theta + \cos^2 \theta$ to get

$$ 2 \sin \theta \cos \theta - 2 \cos \theta \sin \theta = 0$$

So $\sin^2 \theta + \cos^2 \theta$ is constant. Plugging in $\theta = 0$ shows that constant is $1$.

Answer 8

Well it comes directly from the Pythagorean theorem. We know that in a right triangle, $\cos {\theta}=\frac{h}{r}$ and $\sin{\theta}=\frac{v}{r}$, $h$ is short for horizontal and $v$ for vertical, $r$ is the hypotenuse.

Now, from the Pyth. theorem

$$r^2=v^2+h^2=r^2 \sin^2{\theta}+r^2 \cos^2{\theta} \Leftrightarrow \cos^2{\theta}+\sin^2{\theta}=1$$

By the way, the Pythagorean theorem is one of the oldest theorems of mathematics. Archaelogists have discovered it inscribred in stones in excavations in Babylon!

Answer 9

We can define(!) the (first only $\mathbb R\to\mathbb R$) functions $\sin$ and $\cos$ via $\exp(it)=\cos t+i\sin t$ and the (complex) exponential as unique(!) solution of the differential equation $f'(z)=f(z)$ with $f(0)=1$. We need only a few properties of $\exp$ that quickly follow from uniqueness of the solution:

• Since $z\mapsto\frac1{\exp a}\exp(z+a)$ is also a solution whenever $\exp(a)\ne 0$, we conclude by uniqueness that $\exp(a+b)=\exp(a)\exp(b)$ whenever $\exp(a)\ne0$.
• Specifically, $\exp(a)=0$ implies $\exp(a/2)=0$, hence $\exp(2^{-n}a)=0$. As $\exp(0)\ne0$ and $2^{-n}a\to 0$ and $\exp$ is continous, we conclude $\exp(a)\ne0$ for all $a$. Therefore $\exp(a+b)=\exp(a)\exp(b)$ for all $a,b$.
• Since $z\mapsto\overline{\exp(\overline z)}$ is also a solution, we conclude $\exp\overline z =\overline{\exp z}$ for all $z$.

This makes $$ \begin{align}\cos^2t+\sin^2t&=(\cos t+i\sin t)(\cos t-i\sin t)\\ &=\exp(it)\cdot\overline{\exp(it)}\\ &=\exp(it)\cdot\exp(\overline{it})\\ &=\exp(it)\cdot\exp(-it)\\&=\exp(it-it)\\&=\exp(0)\\&=1.\end{align}$$

Answer 10

$\mathbb{}$$\mathbb{}$$\mathbb{}$Hint:

Answer 11

Going from the opposite/hypotenuse and adjacent/hypotenuse definitions:

Let $\theta\in\left[0,\frac{\pi}{2}\right]$ be an angle (in radians, of course) in a right triangle. Let $a$ be the length of the side of a triangle opposite from the angle $\theta$, $b$ the length of the side adjacent to the angle, and $c$ the length of the hypotenuse. Then, $$\sin^{2}\theta+\cos^{2}\theta=\left(\frac{a}{c}\right)^{2} + \left(\frac{b}{c}\right)^{2} = \frac{a^{2}}{c^{2}}+\frac{b^{2}}{c^{2}}=\frac{a^{2}+b^{2}}{c^{2}}=\frac{c^{2}}{c^{2}}=1.$$

To get this result for $0\leq\theta\leq 2\pi$, note that the higher angles only determine the sign of $\sin$ and $\cos$ when a right triangle is formed by going out some length $c$ at angle $\theta$ in the plane and dropping a line perpendicular to the $x$-axis, and since the sign of $\sin$ and $\cos$ don't matter when squaring, the result still holds. To extend the result further to all $\theta\in\mathbb{R}$, note that we just extend the values of $\sin$ and $\cos$ with period $2\pi$ so that we can use any $\theta\in\mathbb{R}$, and it holds trivially.

Answer 12

On one hand, $$ \int_0^x\sin(x)\cos(x)dx= \int_0^x\sin(x)d(\sin(x))dx= \frac{1}{2}\sin^2(x), $$ On the other hand, $$ \int_0^x\sin(x)\cos(x)dx= -\int_0^x\cos(x)d(\cos(x))dx=- \frac{1}{2}\cos^2(x)+ \frac{1}{2}, $$ Hence, by subtraction, we will have that, $$ 0= \frac{1}{2}\sin^2(x)+ \frac{1}{2}\cos^2(x)- \frac{1}{2} $$ or, equivalently, $$ \sin^2(x)+\cos^2(x)=1. $$ I have not seen this proof elsewhere. It is fun.

Answer 13

Proof by using Euler's theorem: $e^{i\theta}=(\cos\theta+i\sin\theta)$

We know that $i^2=-1$, hence $$\color{red}{\cos^2\theta+\sin^2\theta}$$ $$=\cos^2\theta-i^2\sin^2\theta$$ $$=(\cos\theta)^2-(i\sin\theta)^2$$ $$=(\cos\theta+i\sin\theta)(\cos\theta-i\sin\theta)$$ $$=(e^{i\theta})(e^{-i\theta})=e^0=\color{red}{1}$$

Answer 14

Here are two proofs using only the angle sum identities, the fact the trig functions are periodic, and their values at $0$. It is inspired on the connection to rotations and the fact that rotations don't change the sizes of things, but do not actually assume that connection.

Define the matrix

$$ A(\theta) = \left( \begin{matrix} \cos(\theta) & \sin(\theta) \\ -\sin(\theta) & \cos(\theta) \end{matrix} \right) $$

By the angle addition formula, we see that $A(\theta + \varphi) = A(\theta) A(\varphi)$; in particular, $A(n \theta) = A(\theta)^n$.

There are arbitrarily large integer multiples of $\theta$ that are arbitrarily close to integer multiples of $2 \pi$, which gives

$$ A(\theta)^n = A(n \theta) \approx I $$

where $I$ is the identity matrix. By taking determinants, we get

$$ (\cos(\theta)^2 + \sin(\theta)^2)^n \approx 1$$

for arbitrarily large $n$; since the determinant is a real nonnegative number, the only possibility is that

$$ \cos(\theta)^2 + \sin(\theta)^2 = 1$$

---

To get the details right, we select sequences of integers $a_n, b_n$ with

$$ \lim_{n \to \infty} a_n \theta - 2 \pi b_n = 0 $$ $$ \lim_{n \to \infty} a_n = +\infty $$

e.g. this can be done by continued fractions. Then,

$$ \lim_{n \to \infty} A(a_n \theta) = \lim_{n \to \infty} A(a_n \theta - 2 \pi b_n) = A(0) = I$$

and consequently

$$ \lim_{n \to \infty} (\det A(\theta))^{a_n} = 1 $$

---

Another method in the same vein is to also define vectors

$$ v(\theta) = \left( \begin{matrix} \sin(\theta) \\ \cos(\theta) \end{matrix} \right) $$

so that $A(\theta) v(\varphi) = v(\theta + \varphi)$

However, we know that for every angle $\theta$:

$$\frac{1}{2} \leq \max(\sin(\theta)^2, \cos(\theta)^2) \leq 1 $$

In particular, we have

$$ \frac{1}{2} \leq \| v(\theta) \| \leq 2 $$

and furthermore, the $v(\theta)$ span $\mathbb{R}^2$.

By comparing the lengths of $v(\varphi)$ and $A(\theta) v(\varphi)$, we know that all of the eigenvalues of $A(\theta)$ must have magnitude lying between $1/2$ and $2$.

However, this remains true for $A(\theta)^n$, and consequently, all of the eigenvalues of $A(\theta)$ must be roots of unity, and thus the determinant is either $1$ or $-1$, and it can't be $-1$.

Answer 15

Suppose you have a circle with radius r centered at the origin. Using the $ x,y,r$ definitions of $\cos(\theta)$ and $\sin(\theta)$, we have that a point on our circle $(x,y)$, has $x=r\cos(\theta)$ and $y=r\sin(\theta)$. By Pythagorean Theorem, we have $(r\cos\theta)^2+(r\sin\theta)^2 = r^2$ which implies $\cos^2(\theta)+\sin^2(\theta) = 1$

Answer 16

Here is a nice proof by squaring the infinite Taylor series of $\sin x$ and $\cos x$.

The proof:

$$\sin x=\frac{x}{1}-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+...=\sum_{n=0}^{\infty}(-1)^{n}\frac{x^{2n+1}}{(2n+1)!}\\\\\sin^2x=x^2-x^4\left (\frac{1}{1!3!}+\frac{1}{3!1!}\right )+x^6\left (\frac{1}{1!5!}+\frac{1}{3!3!}+\frac{1}{5!1!}\right )-...\\\\\cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+...=\sum_{n=0}^{\infty}(-1)^n\frac{x^{2n}}{(2n)!}\\\\\cos^2x\!=\!1\!-\!x^2\left(\!\frac{1}{0!2!}\!+\!\frac{1}{2!0!}\!\right)\!+\!x^4\left(\!\frac{1}{0!4!}\!+\!\frac{1}{2!2!}\!+\!\frac{1}{4!0!}\!\right)\!-\!x^6\left(\!\frac{1}{0!6!}\!+\!\frac{1}{2!4!}\!+\!\frac{1}{4!2!}\!+\!\frac{1}{6!0!}\!\right)\!+...$$We should have shown that the series for both $\sin x$ and $\cos x$ converge absolutely (since we changed the arrangement), but it's obvious since the absolute value of all terms of $\sin x+\cos x$ add up to $e^x$.$$\sin^2x+\cos^2x=\\=1-x^2\left(\frac{1}{0!2!}-\frac{1}{1!1!}+\frac{1}{2!0!}\right)+x^4\left(\frac{1}{0!4!}-\frac{1}{1!3!}+\frac{1}{2!2!}-\frac{1}{3!1!}+\frac{1}{4!0!}\right)-x^6\left(\frac{1}{0!6!}-\frac{1}{1!5!}+\frac{1}{2!4!}-\frac{1}{3!3!}+\frac{1}{4!2!}-\frac{1}{5!1!}+\frac{1}{6!0!}\right)+...=\\\\=1+\sum_{n=1}^{\infty}(-1)^nx^{2n}\sum_{k=0}^{2n}\frac{(-1)^k\binom{2n}{k}}{(2n)!}$$ Since we can show easily that $\sum_{i=0}^n(-1)^i\binom{n}{i}=0$ by expanding $(1-1)^n$ using Binom's formula. So:$$\sin^2x+\cos^2x=1-0+0-0+...=1$$

I think it's beautiful.