Ergodicity of this Markov Chain

Question

I was recently involved in a debate with a friend over the following graph, and whether it is ergodic or not. In the following diagram, each edge has a strictly positive probability of being travelled on:

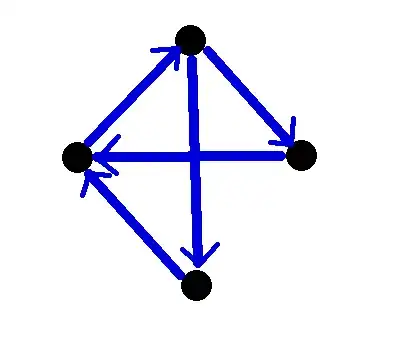
I thought it was ergodic because of the definition from this source, which said that a Markov Chain is ergodic if "if it is possible to eventually get from every state to every other state with positive probability", which is clearly the case here.

However, my friend quoted Wikipedia, alleging that the Markov Chain in question is not ergodic, because it is periodic: he said that all cycles have lengths that are multiples of three.

Who is right, and who is wrong, and why?

Answer 1

If you have drawn the only non-zero transitions then the Markov chain has transition matrix (listing the states in the order north, west, east, south) $$P = \begin{pmatrix} 0 & 0 & \frac{1}{2} & \frac{1}{2}\\ 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 1 & 0 & 0\end{pmatrix}$$ This matrix has the following powers $$P^2 = \begin{pmatrix} 0 & 1 & 0 & 0\\ 0 & 0 & \frac{1}{2} & \frac{1}{2}\\ 1 & 0 & 0 & 0\\ 1 & 0 & 0 & 0\end{pmatrix}$$ $$P^3 = \begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & \frac{1}{2} & \frac{1}{2}\\ 0 & 0 & \frac{1}{2} & \frac{1}{2}\end{pmatrix}$$ $$P^4 = \begin{pmatrix} 0 & 0 & \frac{1}{2} & \frac{1}{2}\\ 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 1 & 0 & 0\end{pmatrix}$$ so note that $P^4=P$. Recall that elements of $P^n$ indexed $(i,j)$ represent the probability of being in state $j$ at time $n$ given that at time $0$ the process was in state $i$. You can see that any time to return to a given state must be a multiple of 3, so the chain is periodic with period 3. (Your friend is right, note that the definition of ergodicity requires the chain to be aperiodic.)