0

Let's say im a guy for ancient Greece and I only have a string and a pencil. And I want to draw a line, the width of the line is the square root of 6. And I only know how to draw a line in the width of real numbers. I've checked out the https://en.wikipedia.org/wiki/Spiral_of_Theodorus but I can't use Pythagoras theorem.

Sorry I couldn't be more specific, if you still don't understand, I'll do my best to explain it again.

Martin Sleziak
  • 53,687
zarko
  • 15
  • By "a string" you mean a straight, unmarked ruler? And by the line's width you mean its length? – DonAntonio Dec 10 '13 at 13:15
  • 1
    Yep, just a normal string. And yes, width = length, forgot the exact term. – zarko Dec 10 '13 at 13:16
  • 1
    possible duplicate of http://math.stackexchange.com/questions/705/compass-and-straightedge-construction-of-the-square-root-of-a-given-line. – lhf Dec 10 '13 at 13:19
  • A picture could help ALOT! My english isnt that good with mathematical terms. – zarko Dec 10 '13 at 13:25

2 Answers2

1

Draw two adjacent segments of size $2$ and $3$. Using the combined segment as diameter, draw a semicircle. Now draw a perpendicular at the point where the two segments meet. That perpendicular defines a segment of length $\sqrt 6$ where it meets the semicircle.

This is the geometric equivalent of the right triangle altitude theorem that says that $h^2=mn$, where $h$ is the altitude of a right triangle with respect to the hypothenuse and $m$ and $n$ are the projections of the sides onto the hypothenuse.

Martin Sleziak
  • 53,687
lhf
  • 216,483
  • Does this method work for any $a,b$ and have the result $\sqrt {a\cdot b}$? – abiessu Dec 10 '13 at 13:21
  • @abiessu, yes, it does. It is also my favorite proof of the AM–GM inequality. – lhf Dec 10 '13 at 13:23
  • A picture could help me alot, couldnt draw the segments and the semicircle right I guess.. – zarko Dec 10 '13 at 13:28
  • @user1885604, see http://en.wikipedia.org/wiki/File:Hoehensatz.svg and http://www.pims.math.ca/~hoek/teageo/Mult-geo/geomean.jpg. – lhf Dec 10 '13 at 13:29
  • So, apparently, we "also" have a compass – DonAntonio Dec 10 '13 at 13:33
  • @DonAntonio, no, from a unit segment, you can draw a segment of size 2 with a compass and so a segment of size 3 by adding a unit segment to that. – lhf Dec 10 '13 at 13:35
  • Yes, the unmarked ruler wasn't on, but the compass is. – DonAntonio Dec 10 '13 at 13:39
  • @DonAntonio: it seems to me that we can't construct much of anything unless we can count on being able to "trap" the string at a point and have it tied to the pencil elsewhere and thus draw a circle of a known radius... And, once being able to draw circles, we can "swap" center and edge points and draw circles which are equal in radius and which are tangent to each others' centers. Having done that, we then have a radius, a diameter, and a diameter+radius as available lengths, and thus we have lengths of "two" and "three" available for further use... – abiessu Dec 10 '13 at 13:43
  • Oh, that's for sure, @abiessu. I was trying to make the OP to give all the relevant info as it seemed something was lacking. Apparently there is a language barrier, I gather now. – DonAntonio Dec 10 '13 at 13:51
  • @lhf , your answers look so simple and easy but I still can understand it much, i'll bring a friend of mine that will try to explain it to me better (using your answer). I'll try to use abiessu answer too. – zarko Dec 10 '13 at 13:51
0

With a string and a pencil, you can measure "one unit", that being the length of the string, or a portion of it. Then you can make a triangle "one unit by one unit." Further, this triangle can be a right triangle since you can perpendicularly bisect a line segment to make the second side. Then you have a hypotenuse side that is $\sqrt 2$ units in length. Because it is isosceles, you can cut it in half along the right angle and get two pieces that have leg lengths of $\frac 1{\sqrt 2}=\frac {\sqrt 2}2$, and so you can get legs as small as desired that are a multiple of $\sqrt 2$.

Next, you can make a second right triangle whose short leg is $\sqrt 2$, and whose hypotenuse is $2\sqrt 2$. Then the long leg has length $\sqrt 6$. Now you have your line of the given length.

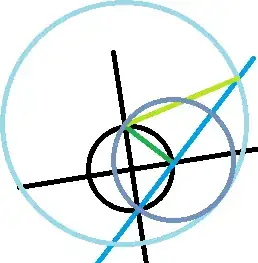
The construction below attempts to demonstrate this process. Begin with one line (black), draw a line perpendicular to it (anywhere), draw a "unit" circle centered at the point of intersection, then the chord (green) between two consecutive intersections of line and circle has length $\sqrt 2$. Draw a circle having this radius (purple), then the diameter will have length $2\sqrt 2$. Draw a perpendicular to the chord (blue) that intersects the (purple) circle's center. Draw a circle (light blue) having radius equal to the diameter of the previous circle (purple), or $2\sqrt 2$. The chord where the (blue) line intersects the (light blue) circle has length $2\sqrt 6$, since the one side associated with the (green, light green, blue) triangle has length $\sqrt 6$.

Construction of sqrt 6

Martin Sleziak
  • 53,687
abiessu
  • 8,115
  • Is there a chance you can add a picture? I kinda understood what you were going for. – zarko Dec 10 '13 at 13:29
  • Not sure if that picture will help, but there it is. – abiessu Dec 10 '13 at 13:44
  • Thank you very much, helped me, still could'nt understand it much but the picture helped alot. I'll ask a friend to help me with this too. – zarko Dec 10 '13 at 13:52