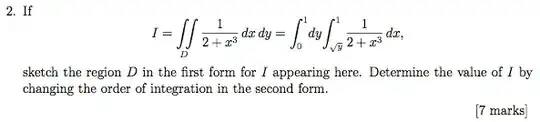
The second form throws me, that the dy appears before the second integral. I have unfortunately little skill for Calculus, and I can't seem to find a similar question online to take example from. All help would be greatly appreciated.
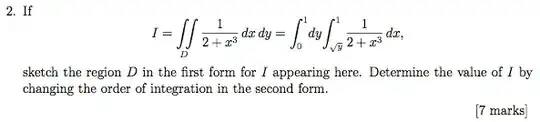
The second form throws me, that the dy appears before the second integral. I have unfortunately little skill for Calculus, and I can't seem to find a similar question online to take example from. All help would be greatly appreciated.
The righthand expression means the same as $$\int_0^1\int_{\sqrt{y}}^1\frac1{2+x^3}dxdy\;,$$ a form that may be more familiar to you.
A double integral is a like a summation over two variables. In your example, the first sum is taken over a variable x, with y fixed. Let's call the resulting sum a function of y -- g(y). The 2nd sum is over a variable y, with the summands or terms equal to different values of g(y).