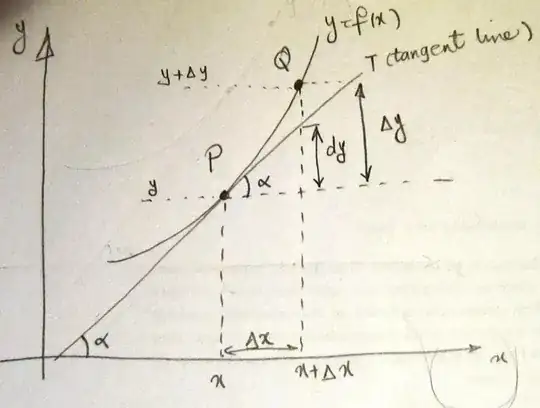
I just started taking a calculus class but I got in late and it had already started like weeks ago, so I'm completely lost.
I believe the teacher uses this same formula in order to get the differential and derivative of a function
$$\lim_{h\to0}\frac{f(x + h) - f(x)}{h}$$
Are they the same? I just need some help to understand it because I can calculate it using this formula (in case it's possible to remove the $h$ from the denominator) but I have no idea of what are these for, I need some examples of when am I going to need them.