2

I would like to approximate a function containing terms of the form $\tanh( B\sqrt{A})$ for small $A$. I have tried doing a Taylor series, but I consistently find that it is not only $A$ that has to be small, but rather $B$ should as well in order to have an accurate approximation.

I can see that this is related to the fact that $\tanh(x)$ asymptotes to 1 for large $x$, so I understand where the issue originates, but I was wondering whether there is any way of getting around this? For example by determining a correction factor that takes the asymptote into account? Can this be done?

Michiel
  • 414
  • About how large is $B \sqrt{A}$? – Antonio Vargas Dec 04 '13 at 18:19
  • Strictly it can be anywhere between 0 and $\infty$, but the range I am interested in is roughly 0 to 50. – Michiel Dec 04 '13 at 19:07
  • So essentially you're asking how to approximate $\tanh x$ on the interval $x \in [0,50]$? Would something like $\tanh x \approx 1 - e^{-1.48x}$ suffice? If not, could you give a little more information about the constraints of your calculation (why you can't just use $\tanh$ itself)? – Antonio Vargas Dec 04 '13 at 19:37
  • How did you come up with $\tanh x \approx 1 - e^{-1.48x}$? If there is some strategy to that which I can also apply to the complete function which contains the $\tanh$ that would be perfect. Using the $\tanh$ itself is not an option because I need to solve an equation of the type $A + \tanh(B \sqrt{A})=1$ explicitly for $A$. – Michiel Dec 04 '13 at 19:42
  • I just found this question, I think that could be helpful for this particular case: http://math.stackexchange.com/questions/107292/rapid-approximation-of-tanhx – Michiel Dec 04 '13 at 19:55
  • Ohh right! I completely forgot about JM's awesome answer there. – Antonio Vargas Dec 04 '13 at 20:30

1 Answers1

1

By definition

$$ \tanh x = \frac{1 - e^{-2x}}{1 + e^{-2x}}, $$

so for $x \gg 1$ (something like $x > 4$) we have

$$ \tanh x \approx 1 - e^{-2x}. $$

Since you're interested in an approximation over a large interval we'll need $\tanh x \approx 1$ for most of it. Additionally, we at least want the approximation to be $0$ at $x = 0$. This suggests we shouldn't modify any of the factors of the terms of $1 - e^{-2x}$, so we'll consider an approximation like

$$ \tanh x \approx 1 - e^{-ax}. $$

Since $\tanh'(0) = 1$ and

$$ \left.\frac{d}{dx}\right|_{x=0} (1-e^{-ax}) = a $$

we'll want $1 < a < 2$. A first guess of $a = 3/2$ is pretty decent in the "eyeball norm" (looking at the plot of the approximation against $\tanh x$), but it looks like a smaller $a$ might be an improvement.

To get an idea of the error for all $x$ we could look at the $L_1$ and $L_2$ error of the approximation over some large interval, say

$$ \int_0^{20} \left|\tanh x - 1 + e^{-ax}\right|\,dx \quad \text{and} \quad \sqrt{\int_0^{20} \left(\tanh x - 1 + e^{-ax}\right)^2\,dx}. $$

Below is a plot of the $L_1$ error in blue and the $L_2$ error in red for $1.35 < a < 1.5$.

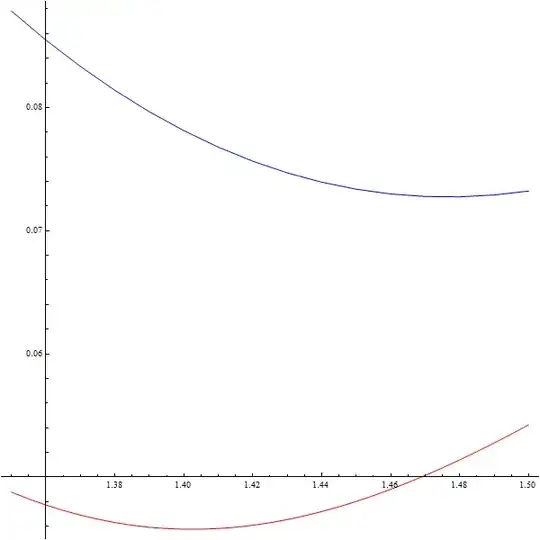
enter image description here

The $L_1$ error has a minimum at $a \approx 1.48$ and the $L_2$ error has one at $a \approx 1.4$, so any $a$ between these two values could be a pretty decent choice.

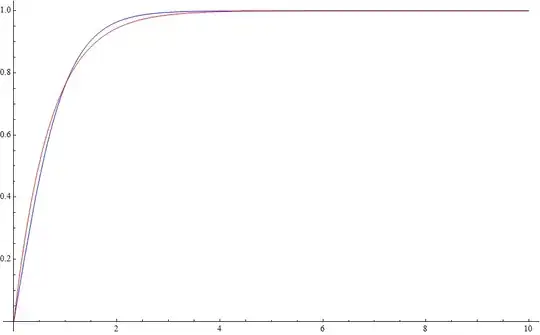
Splitting the difference, here's a plot of $\tanh x$ in blue and $1 - e^{-1.44 x}$ in red.

enter image description here

Antonio Vargas
  • 24,993