An automorphism for a cyclic group needs to take a generator onto a generator.
An automorphism is also part of a symmetry group which for the bounded plane, can only be the identity, a rotation, or a reflection.
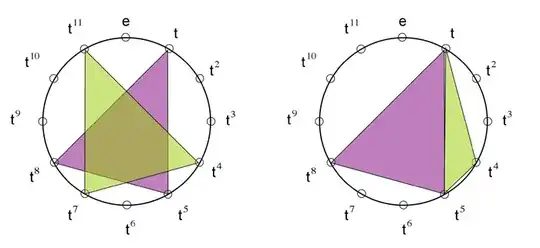
By applying these definition, we obtain a straightforward geometric visualization of $Aut[\mathbb Z_{12}]$.
Start with your $t^1$ generator.
Our first symmetry is identity or mapping everyone onto itself. This is the trivial $1$-automorph which takes $t^1$ to $t^1$. Alternatively, this can be seen as a $360^o$ rotation.
Now, fix a reflection line from $t^0$ to $t^6$. This reflects $t^1$ unto $t^{11}$. Hence the $11$-automorph corresponds to a reflection along the vertical line.
Next, fix a reflection line from $t^3$ to $t^9$. This reflects $t^1$ unto $t^5$. Hence the $5$-automorph corresponds to a reflection along the horizontal line.
Finally, rotate by $180^o$. This takes $t^1$ unto $t^7$. One can alternatively view this as a compound transformation by first reflecting on the vertical (horizontal) and then reflecting on the horizontal (vertical). Either way, this corresponds to the $7$-automorph.
To see this more clearly, map out the generators on your clockface and connect that dots. You will have a rectangle joining $t^1$, $t^5$, $t^7$, and $t^{11}$. Now you can clearly see that the v-reflection, h-reflection, $\pi$-rotation, and $2\pi$-rotation are the only transformations that preserve the rectangle, the only ways to map generators onto generators.
$11$-automorph defines inverses
Note that that the v-reflection, the 11-automorph, defines the inverses of the elements of the group $\mathbb Z_{12} $:
\begin{matrix}
t^{11} = t^{-1}\\
t^7 = t^{-5} \\
t^{11} \not= t^{-5} \not= t^{-7} \\
t^{7} \not= t^{-1} \not= t^{-11}\\
\end{matrix}
We can verify this by considering the automorphisms of the $\mathbb Z_{12}$ subgroups, which should be invariant under the parent group automorphism.
Subgroups $\mathbb Z_{1}$ and $\mathbb Z_{2}$ have trivial $Aut[\mathbb Z_1]$.
Subgroups $\mathbb Z_3, \mathbb Z_4,$ and $\mathbb Z_6$ have non-trivial $Aut[\mathbb Z_2]$.
Now map $Aut[\mathbb Z_{12}]$ onto the non-trivial subgroups and notice that you will always see the $1$-automorph opposite the $11$-automorph and the $5$-automorph opposite the $7$- automorph. You will never see the $1$- and $11$- or the $5$- and $7$- automorphs mapped onto the same the subgroup automorph.
This mapping also gives insight into what it means to be have trivial $Aut[\mathbb Z_1]$. Do the mapping procedure on subgroups $\mathbb Z_1$ and $\mathbb Z_2$ and you'll note that in both cases, $Aut[\mathbb Z_{12}]$ maps to the same generator.
Additive and multiplicative interpretation of $Aut[\mathbb Z_{12}]$
Another observation is that interpreting $Aut[\mathbb Z ]$ as an additive group gives you the generators while interpreting it as a multiplicative group gives you the permutation symmetries. I'm not sure about the wording of the latter but as an example, in the case of $\mathbb Z_{12} $ the multiplicative interpretation means that the ${1,5,7,}$ and $11$-automorphs correspond to:
\begin{matrix}
x \rightarrow x \\
x \rightarrow 5x \\
x \rightarrow 7x \\
x \rightarrow 11x \\
\end{matrix}
Finally, all of this is a refection (pun intended) of the fact that
\begin{matrix}
Aut[\mathbb Z_{12} ] = Aut[\mathbb Z_{8} ]= \mathbb Z_2 \otimes \mathbb Z_2 \end{matrix}
which is the Klein 4-Group with two reflections ($\mathbb Z_2$) plus two rotations ($\mathbb Z_2$)