5

How to fit logarithmic curve to data, in the least squares sense?

I have simple data of the type $(x,y)$, that is 2D. I need to fit curve of the type: $y = c_1 + c_2\ln(x)$. So I have the $x$'s and the $y$'s but I need to learn the $c_1$ and $c_2$ coefficients.

Thanks

Michael Hardy
  • 1
user2381422
  • 179

4 Answers4

8

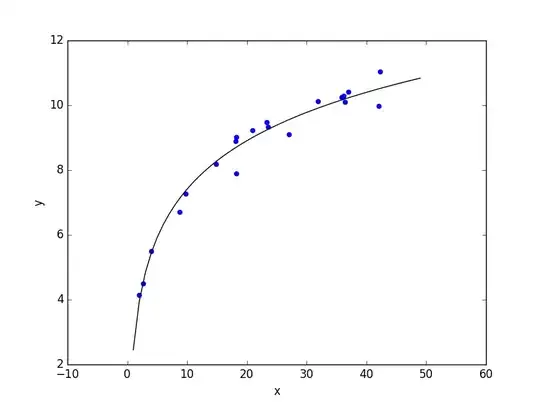
Your equation is: $a\ln(x) + b = y$. So set up matrices like this with all your data:

$$ \begin{bmatrix} \ln(x_0) & 1 \\ \ln(x_1) & 1 \\ &... \\ \ln(x_n) & 1 \\ \end{bmatrix} \begin{bmatrix} a \\ b \\ \end{bmatrix} = \begin{bmatrix} y_0 \\ y_1 \\ ... \\ y_n \end{bmatrix} $$ In other words:

$$Ax = B$$

Where

$$ A = \begin{bmatrix} \ln(x_0) & 1 \\ \ln(x_1) & 1 \\ &... \\ \ln(x_n) & 1 \\ \end{bmatrix} $$ $$ x = \begin{bmatrix} a \\ b \\ \end{bmatrix} $$ and $$ B = \begin{bmatrix} y_0 \\ y_1 \\ ... \\ y_n \end{bmatrix} $$ Now solve for $x$ which are your coefficients. But since the system is over-determined, you need to use the left pseudo inverse: $A^+ = (A^T A)^{-1} A^T$. So the answer is: $$ \begin{bmatrix} a \\ b \\ \end{bmatrix} = (A^T A)^{-1} A^T B $$

Here is some simple Python code with an example:

import matplotlib.pyplot as plt
import numpy as np

TARGET_A = 2
TARGET_B = 3
N_POINTS = 20
MAX_X = 50
NOISE_A = 0.1
NOISE_B = 0.2

# create random data
xs = [np.random.uniform(MAX_X) for i in range(N_POINTS)]
ys = []
for i in range(N_POINTS):
    ys.append((TARGET_A + np.random.normal(scale=NOISE_A)) * np.log(xs[i]) + \
              TARGET_B + np.random.normal(scale=NOISE_B))

# plot raw data
plt.figure()
plt.scatter(xs, ys, color='b')

# do fit
tmp_A = []
tmp_B = []
for i in range(len(xs)):
    tmp_A.append([np.log(xs[i]), 1])
    tmp_B.append(ys[i])
B = np.matrix(tmp_B).T
A = np.matrix(tmp_A)
fit = (A.T * A).I * A.T * B
errors = B - A * fit
residual = np.linalg.norm(errors)

print "solution:"
print "%f log(x) + %f = y" % (fit[0], fit[1])
print "errors:"
print errors
print "residual:"
print residual

# plot fit
fit_x = range(1, MAX_X)
fit_y = [float(fit[0]) * np.log(x) + float(fit[1]) for x in fit_x]
plt.plot(fit_x, fit_y, color='k')

plt.xlabel('x')
plt.ylabel('y')
plt.show()

log fit

Ben
  • 659
  • Good contribution, although for statistical or econometric analysis I would say that spline interpolation could lead to overfitting, so in case the analysis is econometric-statistical related I would recommend fitting a regression over the square root of x, as it is described in another response on this question – Mauro May 04 '23 at 13:22
7

One approach is to replace all of your $x_i$ with $X_i=\ln(x_i)$ and then do usual linear regression with the $(X_i,y_i)$.

2'5 9'2
  • 54,717
  • Which formulas can I use for linear regression fit? Are these ok? http://mathworld.wolfram.com/LeastSquaresFittingLogarithmic.html – user2381422 Dec 04 '13 at 16:40
  • 1
    @user2381422 Yes, note that those are just the regular linear regression formulas, with $\ln(x_i)$ replacing each instance of $x_i$. – 2'5 9'2 Dec 04 '13 at 20:54
1

If such a fit is appropriate then it's done the same way a least-squares fit is done when you have $y=c_1+c_2 w$, but in place of the $w$s you put the values of $\ln x$.

Michael Hardy
  • 1
1

In fact, as long as your functional form is linear in the parameters, you can do a linear least squares fit. You could replace the $\ln x$ with any function, as long as all you care about is the multiplier in front. Section 15.4 of Numerical Recipes, like any other numerical analysis text, will tell you how. Obsolete versions are free.

Ross Millikan
  • 374,822