2

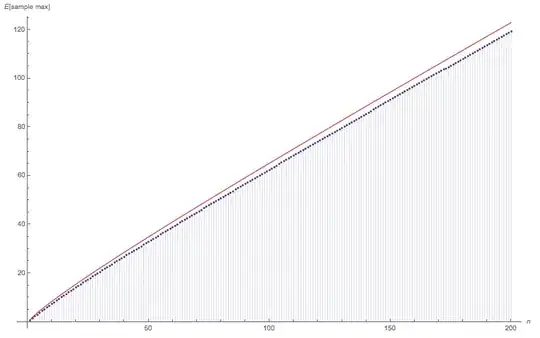
Let $B_i(n,1/2)$ be independent identically distributed binomial random variables. How can one derive lower and upper bounds for the expected value of the maximum of $n$ such random variables? I am especially interested in bounds for large $n$.

In a related question, Expectation of the maximum of gaussian random variables gives an upper bound for the maximum of $n$ gaussian i.i.d $\mathcal{N}(0,\sigma^2)$ random variables of

$$\mathbb{E}[Z] \leq \sigma \sqrt{ 2 \log n} .$$

Is it possible to translate this to my particular problem and can one get a lower bound too?

Community
  • 1
marshall
  • 729
  • 7
  • 22
  • Is it your intention that the number of random variables in your sample $n$ is also equal to the $n$ parameter that defines each $Binomial(n,p)$ parent? That means that if you take a larger sample $n$, the Binomial distribution you are sampling from also changes ... – wolfies Dec 03 '13 at 15:07
  • @wolfies Yes exactly. – marshall Dec 03 '13 at 15:33

2 Answers2

6

Yes it is possible to translate this bound to your particular problem:

The expected value of your binomial random variables is $\mu=\frac{n}{2}$ not $0$, and their standard deviation is $\sigma=\sqrt{\frac{n}{4}}$ so the corresponding upper bound for the maximum is $$ \mathbb{E}[Z] \leq \frac{n}{2}+ \sqrt{\frac{n}{2} \log_e n} .$$ This uses the Gaussian approximation to the binomial, which happens faster than the upper bound being approached.

You cannot get rid of the $\sqrt{\log n}$ term. As an illustration of how good this bound is, if $n=10^6$ then the upper bound would suggest about $502628.3$. In fact the expectation of the maximum value is about $502431.4$ which is about $\frac{n}{2}+ \sqrt{\frac{n}{2.337} \log_e n} $.

Henry
  • 157,058
  • Thank you. Do you know how to get a good lower bound as well? Also, would you mind expanding "which happens faster than the upper bound being approached" a little please? Which fact are you using here? – marshall Dec 03 '13 at 15:33
  • 1
    @marshall: I looked at the first million cases. $\frac{n}{2}+ \sqrt{\frac{n}{3} \log_e n}$ is a lower bound if $n\ge 84$; $\frac{n}{2}+ \sqrt{\frac{n}{2.5} \log_e n}$ is a lower bound if $n\ge 7255$ – Henry Dec 03 '13 at 15:55
2

I was interested to see the accuracy of the upper bound proposed by Henry's neat solution. The following diagram illustrates:

  • Red curve: Henry's upper bound of $\frac{n}{2}+ \sqrt{\frac{n}{2} \log_e n}$
  • The blue dots: the actual exact expectation of the sample maximum, as $n$ increases from 1 to 200.

To my surprise, the upper bound appears to get worse (in an absolute sense) as $n$ gets larger ... not better.

Glorfindel
  • 3,955
wolfies
  • 5,174
  • 3
    My earlier numbers suggest that by the time you get to $n=10^6$, the gap is almost $200$, which is obviously larger in absolute terms than for small $n$, but a smaller proportionate error – Henry Dec 04 '13 at 10:17