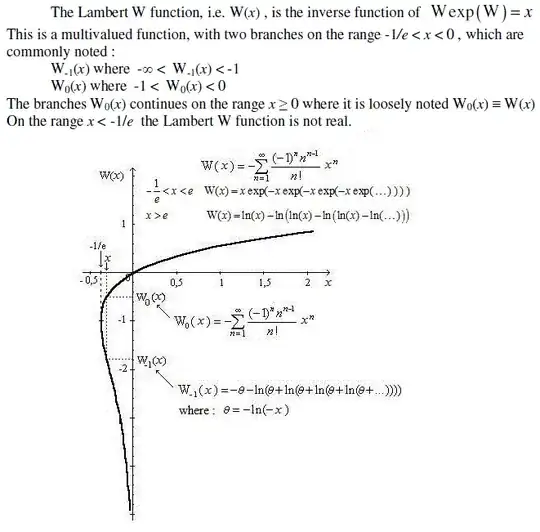
Are there other power series for the Lambert W function than this one?

Question

Are there other known power series for the Lambert W function, other than this one:

$$W(x) = x-x^2+\frac{3 x^3}{2}-\frac{8 x^4}{3}+\frac{125 x^5}{24}-\frac{54 x^6}{5}+\frac{16807 x^7}{720}-\frac{16384 x^8}{315}+\frac{531441 x^9}{4480}-\frac{156250 x^{10}}{567}+\frac{2357947691 x^{11}}{3628800}-\frac{2985984 x^{12}}{1925}+O\left(x^{13}\right)$$

Series[LambertW[x], {x, 0, 12}]

---

Edit 30.11.2013:

Is this a valid generalization to any z?

$$W(z) = \text{Log}[z]+\frac{(-2-\text{Log}[z]) (z-z \text{Log}[z])^2}{2 (1+\text{Log}[z]) (z+z \text{Log}[z])^2}+\frac{z-z \text{Log}[z]}{z+z \text{Log}[z]}+\frac{(z-z \text{Log}[z])^3 \left(9+8 \text{Log}[z]+2 \text{Log}[z]^2\right)}{6 (1+\text{Log}[z])^2 (z+z \text{Log}[z])^3}+\frac{(z-z \text{Log}[z])^4 \left(-64-79 \text{Log}[z]-36 \text{Log}[z]^2-6 \text{Log}[z]^3\right)}{24 (1+\text{Log}[z])^3 (z+z \text{Log}[z])^4}+\frac{(z-z \text{Log}[z])^5 \left(625+974 \text{Log}[z]+622 \text{Log}[z]^2+192 \text{Log}[z]^3+24 \text{Log}[z]^4\right)}{120 (1+\text{Log}[z])^4 (z+z \text{Log}[z])^5}+\frac{(z-z \text{Log}[z])^6 \left(-7776-14543 \text{Log}[z]-11758 \text{Log}[z]^2-5126 \text{Log}[z]^3-1200 \text{Log}[z]^4-120 \text{Log}[z]^5\right)}{720 (1+\text{Log}[z])^5 (z+z \text{Log}[z])^6}+...$$

Mathematica:

Clear[x, a, nn, b, z]
nn = 6;
a = Series[Exp[-x], {x, N[Log[z], 50], nn}];
b = Normal[InverseSeries[Series[x/a, {x, 0, nn}]]];
x = z;
b = b
z = Range[4]
N[b, 20]

---

These numbers appear to be found in the oeis: http://oeis.org/A042977 and the result is known.

Answer 1

$\def\P{\operatorname P}\def\W{\operatorname W}\def\E{\operatorname E}$ Concerning the first question, we use Dirac $\delta(x)$ and its Legendre P$_v(x)$ representation

$$\frac1{\W(x+1)+1}=\int_a^b e^t\delta(t e^t-1-x)dt=\sum_{n=0}^\infty\left(n+\frac12\right)\P_n(x)\int_a^be^t\P_n(te^t-1)dt;0\le|ae^a|<|be^b|\le1,|x|\le1$$

Convergence based on $a,b$ is hard to determine. Now expand P$_n(y)$ with the Pocchammer symbol $(x)_y$:

$$\frac1{\W(x+1)+1}=\sum_{n=0}^\infty\sum_{k=0}^n\left(n+\frac12\right)\frac{(-1)^n(-n)_k(n+1)_k}{2^kk!^2}\P_n(x)\int_a^b e^{(k+1)}t^kdt$$

Therefore we use the exponential integral E$_v(x)$

$$\boxed{\W(x)=-\frac1{\sum\limits_{n=0}^\infty\sum\limits_{k=0}^n\left(n+\frac12\right)\frac{(-1)^n(-n)_k(n+1)_k}{2^kk!^2}\P_n(x-1)\left.\left[t^{k+1}\E_{-k}(-(k+1)t)\right]\right|_a^b }-1}$$

Although slow, it works. A simpler idea uses the lower incomplete gamma function, $a=0$:

$$\boxed{\W(x)=\frac1{\sum\limits_{n=0}^\infty\sum_{k=0}\limits^n\left(n+\frac12\right)\frac{(-1)^n(-n)_k(n+1)_k}{2^kk!^2(-k-1)^{k+1}}\P_n(x-1)\gamma(k+1,-(k+1)b)}-1}$$

Graph of $\W(x)-(n=20$ approximation $)\approx0$:

Both series have interchangeable sums if $k$’s upper bound is $\infty$. For whatever reason, graphing any more terms is chaotic either due to the series or computational limits.

Answer 2

About the LambertW function :

From page 13 in https://fr.scribd.com/doc/34977341/Sophomore-s-Dream-Function