3

With the given parameters $a$, $b$, $c$, and $d$ I'm looking for a solution of the formula $(a + nb)\mod c < d$. The smallest positive $n$ is the value I want to determine.

I can easily solve this iteratively by counting $n$ upwards and perform a simple test but this can take a lot of time and probably won't terminate at all (e. g. if $b = c$ and $a > d$).

This problem also has a graphical representation (actually that's where it originated) which looks roughly like the picture below. Graphically, the question boils down to: When does the blue ray hit the first red obstacle?

ray in grid

mathematics2x2life
  • 13,322
Alfe
  • 951
  • Thanks for giving my post some decent tags, @Willie Wong. I wasn't sure which would fit this problem best. – Alfe Nov 26 '13 at 11:20
  • What types of numbers are $a,b,c,d$? Are they integers? rationals? or are they allowed to be arbitrary reals? You can always divide by $c$ to get the equivalent problem $(A + n B) \mod 1 < D$ if you care about the degrees of freedom. – Willie Wong Nov 26 '13 at 11:22
  • It's a raytracing problem. The parameters are arbitrary reals. Yes, dividing by $c$ reduces complexity but does not solve the problem. (At least I don't see how.) – Alfe Nov 26 '13 at 11:27
  • After the division by $C$, if $B$ is irrational then by the equidistribution theorem the sequence must terminate. But we have no bounds on $n$ directly. On the other hand, if it is a raytracing problem and it sounds like you are doing this on a computer, isn't the problem effectively for rational numbers? – Willie Wong Nov 26 '13 at 11:41
  • Yes, this is computer stuff and effectively of interest to me is only the solution for floating point numbers (so just a tiny subset of the rational numbers). Currently I'm doing this iteratively which is a slow solution and needs to abort after a given limit if no solution is found then. It is similar to creating a graphical representation of a Mandelbrot set. I hope to get a much faster solution if I do not need to iterate. – Alfe Nov 26 '13 at 11:46

2 Answers2

1

Edit: oops, my original version assumed that $d < m$, which as Alfe points out may not be the case. Let me edit.

Okay, since this is a computer problem, the parameters are effectively rational and so by multiplying through by the common denominator we can transform to the equivalent problem for integers. So now we will just assume that $a,b,c,d$ are integers. Let $m$ be the largest common denominator $\mathrm{gcd}(b,c)$.

Without loss of generality we can assume that $c > a > d$. (If $a > c$ replace it by $a \mod c$. If $d >a$ then $0$ is the solution.)

The problem can be equivalently stated as finding the smallest $n$ such that $nb \mod c \in [c-a, c-a + d)$.

Therefore

  1. The problem only has a solution if $\lceil \frac{c-a}{m}\rceil < \lfloor\frac{c-a+d}{m} \rfloor$ or $\lceil \frac{c-a}{m}\rceil = \lfloor\frac{c-a+d}{m} \rfloor < \frac{c-a+d}{m}$, where $\lfloor x\rfloor$ is the largest integer less than $x$ (so the expressions I wrote down are just results of the integer division of $(c-a) / m$ etc. (The second inequality in the second condition is necessary since you specified $<d$. If the condition were $\leq d$ then the second inequality would be not necessary.)
  2. Suppose the problem has a solution, let $k_a = \lceil \frac{c-a}{m} \rceil$, and $k_d = \lfloor \frac{c-a+d}{m}\lfloor$ then $km \in [c-a,c-a+d)$ for every $k \in \{k_a, k_a + 1, \ldots, k_d - 1,k_d\}$. Let $s = b /m$ and let $t = c/m$. What we are looking for then is the smallest $n$ such that $ns \mod t = k$ for one of those $k$s. In other words we have reduced the problem to clockwork arithmetic.
  3. Now, since $m$ is the g.c.d., $s$ and $t$ are coprime by definition. The problem $ns \mod t = k$ in fact has a unique solution $n < t$. This means that $n$ can be computed by first using the extended Euclidean algorithm to compute the multiplicative inverse $s^{-1}$ of $s$ mod $t$, from which we have $n = k s^{-1} \mod t$.
  4. We need to compute $n$ for each $k$ in the list $\{k_a, k_a + 1, \ldots, k_d - 1, k_d\}$. Lastly we take the minimum of all these $n$ to find the minimum value.

I want to end with the remark that it doesn't matter so much that $a$ and $d$ are integers in the problem above. The algorithm given above depends only on $b$ and $c$ being commensurate: that is, it depends only on the existence of a real number $m$ and coprime integers $s,t$ such that $b = sm$ and $c = tm$. In other words, it depends only on $b/c$ being rational.

When $b/c$ is irrational, we know that the smallest $n$ must exist (by the equidistribution theorem). But I do not know of an efficient algorithm or even an effective bound for the size of $n$. (Though some analytic number theorists may be able to tell you more in that case.)

Willie Wong
  • 73,139
  • Whoa. Okay, thank you very much for the elaboration. I scanned it, think I understand it all and now will have to implement each aspect given here. I'm not too happy that in the end the inverse-mod stuff will still need a loop or recursion, but I guess it will have a much smaller number of cycles than plump iterations. When I found this to be working, I will gladly accept this answer! – Alfe Nov 26 '13 at 14:16
  • @Alfe: I am not sure what your application involves, but the slow step (the one using the Euclidean algorithm), depends only on $b$ and $c$. If you can transform your problem into one where $b$ and $c$ remains fixed while $a$ and $d$ are flexible, then you can get some computational savings from not computing the inverse every time. But if $b$ and $c$ (more precisely, the ratio $b/c$) changes between each instance the code is run, then I'm afraid that this is likely the best you can do. – Willie Wong Nov 26 '13 at 14:26
  • Also, this MSE question may help – Willie Wong Nov 26 '13 at 14:28
  • I'm afraid that my $b$ is changing all the time. (Raytracing is about tracing lots of rays in different directions.) The other values will stay constant, though, but that won't help much. – Alfe Nov 27 '13 at 09:18
  • Hmm, I do not yet get correct results. I implemented your solution, using the egcd and invmod implementations I found at http://is.gd/LyCJ2Q . I assume to have a result (so I don't test first), and straight forward compute the values as you stated: $m = \gcd(b, c)$, $k = (c-a) / m + 1$, $s = b / m$, $t = c / m$, $n = k * s^{-1} \mod t$. But for integer values 5, 1, 10, 3 I get the result 6 (one could argue that 5 should result, but off-by-one at a border is fine for me), but for values 500, 101, 1000, 300 I get the result 801 (which obviously is wrong). – Alfe Nov 27 '13 at 14:28
  • Examining your answer in more detail I saw that the value $d$ does not appear anymore within the implementation at all; it only appears in the existence restriction (which I do not use because for my unround values a solution always should exist). But at least when computing it, the value $d$ should be part of the computation, shouldn't it? – Alfe Nov 27 '13 at 14:32
  • Maybe I'm misunderstanding something; my Python code for computing this can be found at http://pastebin.com/6FW6sAE6 . – Alfe Nov 27 '13 at 14:34
  • @Alfe: Indeed your code looks okay. Looking at your values I realised that I made the unreasonable assumption that $d < m$, which would imply that in each "cycle" the ray only hits the region you want once; this is because I kept thinking of $d$ as approximation error and assumed it to be smaller than the "unit". Evidently that was a poor assumption! Sorry about that. The off-by-one error is due to me writing floor(x) +1 when I should've written ceil(x). Again, apologies. I've fixed both the errors. Let me know if there are still bugs! – Willie Wong Nov 27 '13 at 15:57
  • For the modified version with (500,101,1000,300), we have that m = 1, k_a = 500, k_d = 800, s = 101, t = 1000. So the inverse $s^{-1} = 901$. Now, for k between 500 and 800, the minimum for n is reached when k = 505, with 505 * 901 mod 1000 = 5 mod 1000 = 5. Though with the incorrect pseudocode I gave you before, you should've found 501 * 901 mod 1000 = 401, and not 801, so there is something else wrong with the code. (Note that 801 = 901 * 901 mod 1000, so I really don't see where it comes from!) – Willie Wong Nov 27 '13 at 16:20
  • Now I get useful results! (There's something strange, sometimes the results don't seem to match my original ones, but I didn't investigate on that any further.) But, of course, now you've blown up the computation massively (I have to compute each $k_i$ now). Because I typically limit my dumb computation to at most some hundred cycles, your current version is way slower than the dumb one then. For much higher results your solution of course is better but for my situation unfortunately this doesn't help :-( Any (maybe different) idea on how to speed up things? – Alfe Nov 27 '13 at 18:48
  • I found the "strage" thing, it was about negative $b$, so I could fix that with taking it mod $c$, now the results always match the original. But the performance still is an issue. I hoped for fastening up things by getting a simpler version without the need to loop, and now only got a better but slower version (depending on usecase of course, but this is mine). I will leave this answer unaccepted for a week or so (and will accept eventually if nothing better shows up); but maybe someone else has an idea which actually speeds up my algorithm. – Alfe Nov 28 '13 at 08:48
  • @Alfe: it is probably possible to introduce speedups by using, instead of exactly gcd(b,c) some approximate variants that gives large m, which will reduce the number of k_i needed. After finding an approximate solution n one can then try to verify it (which is much less computationally intensive). If it fails, then switch to a finer approximation that reduces m. If you are lucky, optimising may be able to give you a speedup for "most cases" at the cost of dramatically slowing things down for the "bad edge cases". But I don't have the expertise to exactly compute the tradeoffs here. – Willie Wong Nov 28 '13 at 09:19
  • I'm considering using well-chosen ratios of $d$ and $c$; since this is a design issue, I can choose those rather freely, so maybe I can speed up things by ensuring that $\gcd(d, c) = d$. Also, I can iterate for, say, twenty times, and then switch to your algorithm to find results for the points farther away. Btw, in case you're interested: this is used for creating Escher-inspired pictures. See http://is.gd/KBJ4eC and http://i.imgur.com/bsW6k9h.png . – Alfe Nov 28 '13 at 09:56
  • Ah! I see what you are trying to do! Neat pictures, by the way. But if you have some dispersion (or whatever you call it in ray tracing, that makes faraway objects less visible), couldn't you just brute-force say 30 steps and cut-off? But this is getting off topic. :-) – Willie Wong Nov 28 '13 at 10:07
  • That's what I do. I hoped to speed it up by some fancy one-liner without looping. – Alfe Nov 28 '13 at 11:17
1

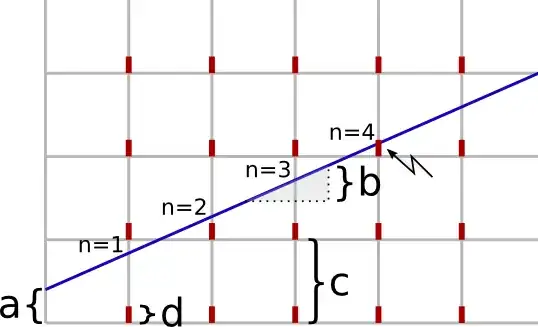
Now that I see what you are trying to do, I can offer a different bit of advice!

Your goal is to compute the mapping from $b$ to $n$ for every $b$. So instead of solving $n$ from given $a,b,c,d$, you should solve for $b$ given $a,c,d,n$ and "fill in the mapping". (Basically we compute the inverse mapping, which I am pretty sure is computationally simpler.)

In fact, for each $n$ you can produce a "mask": the set of angles which will see a block at distance $n$. And this is easy to solve. You are looking for the values $b$ satisfying

$$ nb \in [mc,mc+d) $$

for some $m$. This can be solved as

$$ b \in [\frac{mc}{n}, \frac{mc+d}{n}) $$

for $m$ an integer. And in particular their end points can be explicitly computed!

This also makes your reference to Mandelbrot set make more sense! To render your ray tracing, you probably want to start from the limit of visibility (with the $n$ and $m$ corresponding to the furthest you can see), compute the corresponding intervals $b$, paint them in, and then gradually drop $m,n$, overwriting the previous $b$ if necessary (nearer objects block out farther objects).

Basically the idea is to ignore the notion of the first $n$. Instead, for each block determine the angles $b$ which would see the block, if there were nothing else in the way. If you start from the farthest block and move closer, you will be able to decrease the corresponding $n$ value when a block blocks another block.

Community
  • 1
Willie Wong
  • 73,139
  • That's a whole different approach, basically switching from raytracing to standard triangle rendering as video games do it today. I find that rather boring. I chose raytracing because I viewed the resulting image from the same perspective as a Mandelbrot set in which zooming into the minutest details is possible. (I can do that as well of course.) I also rendered a high-res image in size A0 with 300 dpi (i. e. ≈ 15000 × 10000 pixels), so I would be hard pressed to find a true upper limit for $n$. Also, in raytracing I can easily combine such a grid with various other objects. – Alfe Nov 28 '13 at 11:38