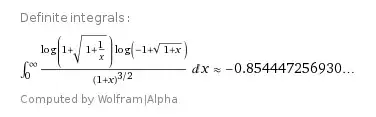Integral $\int_0^\infty\frac{\ln\left(\sqrt{x+1\vphantom{x^0}}-1\right)\,\ln\left(\sqrt{x^{-1}+1}+1\right)}{(x+1)^{3/2}}dx$

Question

Another integral similar to my previous question: $$\int_0^\infty\frac{\ln\left(\sqrt{x+1\vphantom{x^0}}-1\right)\,\ln\left(\sqrt{x^{-1}+1}+1\right)}{(x+1)^{3/2}}dx$$ Can someone suggest how to evaluate it? Is there a closed form?

Answer 1

Yes, there is a closed form: $$\frac{\pi^2}3-\ln^22-4\,G,$$ where $G$ is the Catalan constant: $$G=-\int_0^1\frac{\ln x}{x^2+1}dx.$$

Answer 2

Is known that

\begin{cases} \int\limits_0^1 \dfrac {y\,\mathrm dy}{(1+y^2)^2} = \dfrac14\\ \int\limits_0^1 \ln y \dfrac {y\,\mathrm dy}{(1+y^2)^2} = -\dfrac{\ln2}4\\ \int\limits_0^1 \ln (1-y^2) \dfrac {y\,\mathrm dy}{(1+y^2)^2} = -\dfrac{\ln2}4\\ \int\limits_0^1 \ln (1+y) \dfrac {y\,\mathrm dy}{(1+y^2)^2} = \dfrac{\pi-2\ln2}{16}. \tag1\end{cases}

Substitution $$x=\dfrac{4y^2}{(1-y^2)^2},\quad \sqrt{x+1\mathstrut} = \dfrac{1+y^2}{1-y^2},\quad \sqrt{x^{-1}+1\mathstrut} = \dfrac{1+y^2}{2y},\quad y\in(0,1)$$

allows to write \begin{align} &I=\int_0^\infty\frac{\ln\left(\sqrt{x+1\large\mathstrut}-1\right)\,\ln\left(\sqrt{x^{-1}+1\large\mathstrut}+1\right)}{(x+1){\Large\!^{^{\normalsize\,^3/_2}}}}\mathrm dx\\[8pt] &=\int_0^1\ln\dfrac{2y^2}{1-y^2}\,\ln\dfrac{(1+y)^2}{2y}\,\dfrac{(1-y^2)^3}{(1+y^2)^3}\ \dfrac{8y(1-y^2)+16y^3}{(1-y^2)^3}\,\mathrm dy\\[8pt] &=8\int_0^1\left(\ln2+\ln\dfrac{y^2}{1-y^2}\right)\,\left(\ln2+\ln\dfrac{(1+y)^2}{4y}\right)\,\dfrac{y\ \mathrm dy}{(1+y^2)^2}\\ &=8\ln2\int_0^1\left(-\ln2+\ln y+2\ln(1+y)-\ln(1-y^2)\Large\mathstrut\right)\,\dfrac{y\ \mathrm dy}{(1+y^2)^2}\\ &+8\int_0^1\ln\dfrac{y^2}{1-y^2}\,\ln\dfrac{(1+y)^2}{4y}\,\dfrac{y\ \mathrm dy}{(1+y^2)^2}\\ &=(-2\ln2-2\ln2 +\pi-2\ln2+2\ln2)\ln2+8\int_0^1\ln\dfrac{y^2}{1-y^2}\,\ln\dfrac{(1+y)^2}{4y}\,\dfrac{y\ \mathrm dy}{(1+y^2)^2}, \end{align} $$I=(\pi-4\ln2)\ln2+I_1,\quad\text{where}\quad I_1=8\int_0^1\ln\dfrac{y^2}{1-y^2}\,\ln\dfrac{(1+y)^2}{4y}\,\dfrac{y\ \mathrm dy}{(1+y^2)^2}.\tag2$$

By parts: \begin{align} &I_1=8\int_0^1\,\ln\dfrac{(1+y)^2}{4y}\,\mathrm d\int_0^y\ln\dfrac{y^2}{1-y^2}\,\dfrac{y\ \mathrm dy}{(1+y^2)^2}\\[8pt] &=8\left.\left(\ln\dfrac{(1+y)^2}{4y}\,\int_0^y\ln\dfrac{y^2}{1-y^2}\,\dfrac{y\ \mathrm dy}{(1+y^2)^2}\right)\right|_{\,0}^{\,1}\\[8pt] &-8\int_0^1\,\left(\ln\dfrac{(1+y)^2}{4y}\right)'\left(\int_0^y\ln\dfrac{y^2}{1-y^2}\,\dfrac{y\mathrm dy}{(1+y^2)^2}\right)\mathrm dy\\[8pt] &= 0 - 2\int_0^1\,\left(\dfrac2{1+y}-\dfrac1y\right)\left(\dfrac{4y^2}{1+y^2}\ln y +\dfrac{1-y^2}{1+y^2}\ln(1-y^2) - \ln(1+y^2)\right)\,\mathrm dy\\[8pt] &=2\int_0^1\left(\dfrac{1-y}{y(1+y)}\left(\dfrac{4y^2}{1+y^2}\ln y +\dfrac{1-y^2}{1+y^2}\ln(1-y^2)\right)-\left(\dfrac2{1+y}-\dfrac1y\right) \ln(1+y^2)\right)\mathrm dy\\[8pt] &= 8\int_0^1\,\dfrac{y(1-y)}{(1+y)(1+y^2)}\ln y\,\mathrm dy +2\int_0^1\,\dfrac{(1-y)^2}{y(1+y^2)}\ln(1-y)\,\mathrm dy\\[8pt] &+2\int_0^1\,\dfrac{(1-y)^2}{y(1+y^2)}\ln(1+y)\,\mathrm dy -2\int_0^1\,\left(\dfrac1y-\dfrac2{1+y}\right)\ln(1+y^2)\,\mathrm dy \end{align} (see also Wolfram Alpha undefined integral).

At last - calculating of the remaining integrals and final summation: \begin{align} &I=\pi\ln2-4\ln^22 + 8\left(\dfrac{\pi^2}{12}-G\right) +2\left(2G-\dfrac\pi{12}(2\pi+3\ln2)\right)\\[4pt] &+2\,\dfrac\pi{12}(\pi-3\ln2) -2\left(\dfrac{\pi^2}{24} -2\left(\dfrac34\ln^2 2 - \dfrac{\pi^2}{48}\right)\right),\\[8pt] &\color{brown}{\boxed{\ \mathbf{I=\dfrac{\pi^2}3 - \ln^2 2 -4G \approx -0.85444\,72569.}\ \large\mathstrut}}\\ \end{align} (see also Wolfram Alpha 1st integral, 2nd integral, 3rd integral, 4th integral, 5th integral)

Obtained result corresponds with the exact value.

Answer 3

$$\small \mathcal I=\int_0^\infty\frac{\ln\left(\sqrt{1+x\vphantom{x^0}}-1\right)\,\ln\left(\sqrt{1+x^{-1}}+1\right)}{(1+x)^{3/2}}dx\overset{1+x=\frac{1}{t^2}}=2\int_0^1 \ln\left(\frac{1}{t}-1\right)\ln\left(\frac{1}{\sqrt{1-t^2}}+1\right)dt$$ $$\small \ln\left(\frac{1}{\sqrt{1-t^2}}+1\right)=\ln\left(1+\sqrt{1-t^2}\right)-\frac12 \ln(1-t^2)=\ln\left(\frac{1+\sqrt{1-t^2}}{t}\right)-\frac12 \ln\left(\frac{1}{t^2}-1\right) $$

$$\small \Rightarrow \mathcal I=2\int_0^1 \ln\left(\frac{1}{t}-1\right){\ln\left(\frac{1+\sqrt{1-t^2}}{t}\right)}dt-\int_0^1 \ln^2\left(\frac{1}{t}-1\right)dt-\int_0^1 \ln\left(\frac{1}{t}-1\right){\ln\left(\frac{1}{t}+1\right)}dt$$ The reason behind getting $\ln\left(\frac{1+\sqrt{1-t^2}}{t}\right)$ in the place of $\ln\left(\frac{1}{\sqrt{1-t^2}}+1\right)$ is that it's easier to work with the former when integrating by parts since it's derivative is just $-\frac{1}{t\sqrt{1-t^2}}$. $$\mathcal I=2\color{blue}{\mathcal I_1}-\color{green}{\mathcal I_2}-\color{red}{\mathcal I_3}=2\left(\color{blue}{\frac{3\pi^2}{8}-2G}\right)-\color{green}{\frac{\pi^2}{3}}-\left(\color{red}{\ln^2 2+\frac{\pi^2}{12}}\right)=\boxed{\color{chocolate}{\frac{\pi^2}{3}-\ln^2 2-4G}}$$

---

$$\color{blue}{\mathcal I_1}=\int_0^1 \left(t\ln\left(\frac{1}{t}-1\right)-\ln(1-t)\right)'\ln\left(\frac{1+\sqrt{1-t^2}}{t}\right) dt$$ $$\overset{IBP}=\int_0^1 \frac{\ln\left(\frac{1}{t}-1\right)}{\sqrt{1-t^2}}dt-\int_0^1 \frac{\ln(1-t)}{t\sqrt{1-t^2}}dt$$ $$\int_0^1 \frac{\ln\left(\frac{1}{t}-1\right)}{\sqrt{1-t^2}}dt\overset{t=\cos x}=\int_0^\frac{\pi}{2} \ln\left(\sec x-1\right)dx=\int_0^\frac{\pi}{2}\ln(1-\cos x)dx-\color{tomato}{\int_0^\frac{\pi}{2}\ln(\cos x)dx}$$ $$\overset{\color{tomato}{x\to \frac{\pi}{2}-x}}=\int_0^\frac{\pi}{2}\ln\left(1-\cos x\right)dx-\color{tomato}{\int_0^\frac{\pi}{2}\ln(\sin x)dx}=\int_0^\frac{\pi}{2} \ln\left(\frac{1-\cos x}{\sin x}\right)dx\overset{x\to 2t}=2\int_0^\frac{\pi}{4}\ln (\tan t)dt$$ $$\overset{\tan t=x}=2\int_0^1 \frac{\ln x}{1+x^2}dx=2\sum_{n=0}^\infty (-1)^n\int_0^1 x^{2n} \ln xdx=-2\sum_{n=0}^\infty \frac{(-1)^n}{(2n+1)^2}=\color{blue}{-2G}$$

$$\int_0^1 \frac{\ln(1-t)}{t\sqrt{1-t^2}}dt\overset{t=\sin x}=\int_0^\frac{\pi}{2} \frac{\ln(1-\sin x)}{\sin x}dx=-\color{blue}{\frac{3\pi^2}{8}}$$ Above follows by plugging $a=\frac{3\pi}{2}$ in here.

---

$$\color{green}{\mathcal I_2}=\int_0^1 \ln^2\left(\frac{1}{t}-1\right)dt=\int_0^\frac12 \left(\frac{1}{t}-1\to \frac1x\right)+\int_\frac12^1\left(\frac{1}{t}-1\to x\right)=2\int_0^1 \frac{\ln^2 x}{(1+x)^2}dx$$ $$=2\sum_{n=1}^\infty (-1)^{n-1}n\int_0^1 x^{n-1}\ln^2 x=4\sum_{n=1}^\infty \frac{(-1)^{n-1}}{n^2}=\color{green}{\frac{\pi^2}{3}}$$

---

$$\color{red}{\mathcal I_3}=\int_0^1 \left(t\ln\left(\frac{1}{t}-1\right)-\ln(1-t)\right)'\ln\left(\frac{1}{t}+1\right)dt\overset{IBP}=\int_0^1 \frac{t\ln\left(\frac{1}{t}-1\right)-\ln(1-t)}{t(1+t)}dt$$ $$=\int_0^1 \frac{\ln\left(\frac{1}{t}-1\right)}{1+t}dt+\int_0^1 \frac{\ln(1-t)}{1+t}dt-\underbrace{\int_0^1 \frac{\ln(1-t)}{t}dt}_{1-t=x}$$ $$t=\frac{1-x}{1+x}\Rightarrow \int_0^1\frac{\ln\left(\frac{1}{t}-1\right)}{1+t}dt=\int_0^1 \frac{\ln 2 +\ln x-\ln(1-x)}{1+x} dx$$ $$\require{cancel}\Rightarrow \color{red}{\mathcal I_3}=\int_0^1 \frac{\ln 2}{1+x}dx+\int_0^1\frac{\ln x}{1+x}dt-\cancel{\int_0^1 \frac{\ln(1-x)}{1+x}dx}+\cancel{\int_0^1 \frac{\ln(1-t)}{1+t}dt}-\int_0^1 \frac{\ln x}{1-x}dx$$ $$=\ln^2 2-\int_0^1 \frac{2x\ln x}{1-x^2}dx\overset{x^2=t}=\ln^2 2-\frac12\int_0^1 \frac{\ln t}{1-t}dt=\color{red}{\ln^2 2+\frac{\pi^2}{12}}$$

Answer 4

To evaluate $$ \int^{\infty}_{0}\frac{\log\left(\sqrt{x+1}-1\right)\log\left(\sqrt{1/x+1}+1\right)}{(x+1)^{3/2}}dx.\tag 1 $$ I will evaluate first $$ I(x)=\int\frac{\log\left(\sqrt{x+1}-1\right)\log\left(\sqrt{1/x+1}+1\right)}{(x+1)^{3/2}}dx\tag 2 $$ and then use limits to find the answer. The evaluation is based on Mathematica program (see Wolfram alpha...etc).

First write $$ I(x)=-2\int\log\left(\sqrt{x+1}-1\right)\log\left(\sqrt{1/x+1}+1\right)\frac{d}{dx}\left(\frac{1}{\sqrt{x+1}}\right)dx. $$ Then using integration by parts we find $$ I(x)=-\frac{2}{\sqrt{x+1}}\log\left(\sqrt{x+1}-1\right)\log\left(\sqrt{1/x+1}+1\right)+ $$ $$ +\int\frac{\log\left(1+\sqrt{1+\frac{1}{x}}\right)}{(1+x)(-1+\sqrt{1+x})}dx+\int\frac{(\sqrt{x^2+x}-x-1)\log\left(-1+\sqrt{1+x}\right)}{x(1+x)^{3/2}}dx= $$ $$ =-\frac{2}{\sqrt{x+1}}\log\left(\sqrt{x+1}-1\right)\log\left(\sqrt{1/x+1}+1\right)+ $$ $$ +\int\frac{\log\left(1+\sqrt{1+\frac{1}{x}}\right)}{(1+x)(-1+\sqrt{1+x})}dx +\int\frac{\log\left(-1+\sqrt{1+x}\right)}{(1+x)\sqrt{x}}dx -\int\frac{\log\left(-1+\sqrt{1+x}\right)}{x\sqrt{1+x}}dx\tag 3 $$ But all three integrals can evaluated with Mathematica and we write for $x>0$

$$ I_1(x)=\int\frac{\log\left(-1+\sqrt{1+x}\right)}{(1+x)\sqrt{x}}dx -\int\frac{\log\left(-1+\sqrt{1+x}\right)}{x\sqrt{1+x}}dx= 2\pi i\cot^{(-1)}(\sqrt{x})- $$ $$ -\frac{1}{2}\log\left(-1+\sqrt{1+x}\right)\left(\log 4+\log\left(-1+\sqrt{1+x}\right)-2\log\left(1+\sqrt{1+x}\right)\right)- $$ $$ -4i\cdot\textrm{Li}\left(2,\frac{1-i\sqrt{x}}{\sqrt{1+x}}\right)+i\cdot\textrm{Li}\left(2,1-\frac{2}{1+i\sqrt{x}}\right)+\textrm{Li}\left(2,\frac{1}{2}\left(1-\sqrt{1+x}\right)\right)+C_1.\tag 4 $$ Also if $y=1/x$, then $$ I_2(x)=\int\frac{\log\left(1+\sqrt{1+\frac{1}{x}}\right)}{(1+x)(-1+\sqrt{1+x})}dx=-\int\frac{\log\left(1+\sqrt{1+y}\right)}{y+1}dy-\int\frac{\log(1+\sqrt{1+y})}{\sqrt{y(y+1)}}dy= $$ $$ =-4i\log( x)\arcsin\left(\sqrt{\frac{1}{2}\left(1+\sqrt{1+x^{-1}}\right)}\right)- $$ $$ -4\arcsin\left(\frac{1}{2}\left(1+\sqrt{1+x^{-1}}\right)\right)^2+\log(x)\log\left(1+\sqrt{1+x^{-1}}\right)- $$ $$ -2\pi i \log\left(1+\sqrt{1+x^{-1}}\right)-2\log\left(1+\sqrt{1+x^{-1}}\right)\log\left(1+\sqrt{1+x}\right)+ $$ $$ 8i\arcsin\left(\sqrt{\frac{1}{2}\left(1+\sqrt{1+x^{-1}}\right)}\right)\log\left(-1+\sqrt{x}+\sqrt{1+x}\right)+ $$ $$ +2\textrm{Li}\left(2,-\sqrt{1+x^{-1}}\right)-4\textrm{Li}\left(2,-\frac{1}{\sqrt{x}}\left(-1+\sqrt{1+x}\right)\right) $$ Hence $$ I(x)=I_1(x)+I_2(x) $$ and we can see easily using Mathematica that $$ \lim_{x\rightarrow\infty}I(x)=-4G-\left(1-\frac{i}{4}\right)\pi^2+2\pi i \log 2-\frac{1}{2}\log^22 $$ Also $$ \lim_{x\rightarrow0}I(x)=\left(-\frac{4}{3}+\frac{i}{4}\right)\pi^2+2\pi i\log 2+\frac{1}{2}\log^22 $$ Hence $$ \int^{\infty}_{0}\frac{\log\left(\sqrt{x+1}-1\right)\log\left(\sqrt{1/x+1}+1\right)}{(x+1)^{3/2}}dx=-4G+\frac{\pi^2}{3}-\log^22 $$ QED