I had asked this question: Characterising Continuous functions some time back, and this question is more or less related to that question.
Suppose we have a function $f: \mathbb{R} \to \mathbb{R}$ and suppose the set $G = \\{ (x,f(x) : x \in \mathbb{R}\\}$ is connected and closed in $\mathbb{R}^{2}$, then does it imply $f$ is continuous?
This Monthly paper has short simple proofs of the following
THEOREM$\ $ TFAE if $\rm\ f: \mathbb R\to \mathbb R\ $ has a closed graph in $\:\mathbb R^2$
(a)$\rm\ \ f\ $ is continuous.
(b)$\rm\ \ f\ $ is locally bounded.
(c)$\rm\ \ f\ $ has the intermediate value property.
(d)$\rm\ \ f\ $ has a connected graph in $\rm\mathbb R^2$.
More generally the result is merely a special case of R. L. Moore's 1920 characterization of a topological line as a locally compact metric space that is separated into two connected sets by each of its points.
Per request, I've appended the proof of the theorem below.
The answer is yes. Here's one way to prove it. (There might be a slicker way, but this seems to work.)
Assume $G$ is connected and closed. Let $a\in\mathbb R$ be arbitrary, and let $\epsilon>0$ be given. Because $(a,f(a)-\epsilon)\notin G$, the fact that the complement of $G$ is open implies that there is a product neighborhood of the form $(a-\delta,a+\delta)\times (f(a)-\epsilon-c, f(a)-\epsilon+c)$ contained in the complement of $G$. This means that $|x-a|<\delta$ implies that one of the following two inequalities holds:
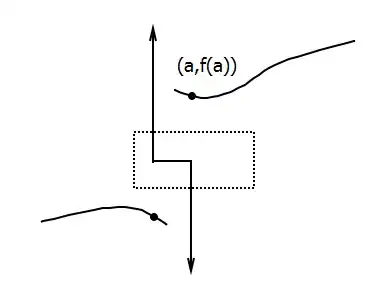
If there is any $x\in (a-\delta,a+\delta)$ so that the second inequality holds, say $f(b)\le f(a)-\epsilon-c$ (without loss of generality, we may assume $b\lt a$), then the graph of $f$ does not intersect the following set:
$$\\{(b,y): y\ge f(a)-\epsilon \\}\cup \\{(x,f(a)-\epsilon): b\le x \le a\\} \cup \\{(a,y): y\le f(a)-\epsilon\\}.$$
(See the diagram below.) This broken line disconnects $G$, contradicting the assumption that $G$ is connected. Therefore inequality (1) holds when $|x-a|<\delta$.
A similar argument shows that $f(x)\lt f(a)+\epsilon$ when $|x-a|<\delta$.
Putting these together, we conclude that $|x-a|<\delta$ implies $|f(x)-f(a)|<\epsilon$, so $f$ is continuous at $a$.
suppose you have a function $f:\mathbb{R} \rightarrow \mathbb{R}$ which is not continuous and its graph is closed and connected. wlog assume f is not continuous at zero and f(0)=0.
first, I want to show that when x approaches zero then either f(x) approaches 0 or goes to infinity. for every b>a>0 let $ X_{a,b} = \{ x>0 \mid a < f(x) < b \} $ . if this set is not empty, then its infimum cannot be 0, because then the closure of the graph will give us that $ a \leq f(0) \leq b $ (you can find a series $a_n \rightarrow 0 \subseteq X_{a,b}$ and a sub-series such that $f(a_{n_i})$ is monotone and thus converges in $R^2$).
now I want to use the connectedness to show that f(x) cannot go to infinity when x goes to zero.
$f$ isn't continuous at zero, so wlog there is an $\varepsilon > 0$ such that $ X_{2\varepsilon, \infty}$ is not empty and its infimum is 0. $X_{\varepsilon, 2\varepsilon}$ has infimum > 0 (if not empty) - denote it by $\delta$. if you have $0 < x_0 < \delta$ such that $ x_0 \notin X_{2 \varepsilon, \infty} $ (and so $f(x_0) < \varepsilon $ ) then you have the open sets $ A = (0, x_0) \times (1.5 \varepsilon, \infty) $ and $ R^2 - \bar A$ which separates the garph of the function.
otherwise, if $ (0,\delta) \subseteq X_{2\varepsilon, \infty} $ then you can take the sets $A = \{x\leq 0 \} \cup (0, \delta/2) \times (-\infty, 1.5 \varepsilon)$ and $R^2 - \bar A$.
Yes, I think so.
First, observe that such $f$ must have the intermediate value property. For suppose not; then there exist $a < b$ with (say) $f(a) < f(b)$ and $y \in (f(a),f(b))$ such that $f(x) \ne y$ for all $x \in (a,b)$. Then $A = (-\infty,a) \times \mathbb{R} \cup (-\infty,b) \times (-\infty,y)$ and $B = (b, +\infty) \times \mathbb{R} \cup (a,+\infty) \times (y,+\infty)$ are disjoint nonempty open subsets of $\mathbb{R}^2$ whose union contains $G$, contradicting connectedness. (Draw a picture.)
Now take some $x \in \mathbb{R}$, and suppose $f(x) < y < \limsup_{t \uparrow x} f(t) \le +\infty$. Then there is a sequence $t_n \uparrow x$ with $f(t_n) > y$ for each $n$. By the intermediate value property, for each $n$ there is $s_n \in (t_n, x)$ with $f(s_n) = y$. So $(s_n, y) \in G$ and $(s_n,y) \to (x,y)$, so since $G$ is closed $(x,y) \in G$ and $y = f(x)$, a contradiction. So $\limsup_{t \uparrow x} f(t) \le f(x)$. Similarly, $\limsup_{t \downarrow x} f(t) \le f(x)$, so $\limsup_{t \to x} f(t) \le f(x)$. Similarly, $\liminf_{t \to x} f(t) \ge f(x)$, so that $\lim_{t \to x} f(t) = f(x)$, and $f$ is continuous at $x$.
