1

Let $f(x) = (\sin \frac{πx}{7})^{-1}$. Prove that $f(3) + f(2) = f(1)$. This is another trig question, which I cannot get how to start with. Sum to product identities also did not work.

Sawarnik
  • 7,284
  • 7
  • 33
  • 74
  • http://math.stackexchange.com/questions/507446/on-the-funny-identity-tfrac1-sin2-pi-7-tfrac1-sin3-pi-7-tf – lab bhattacharjee Nov 18 '13 at 15:22
  • @labbhattacharjee The proofs there are very general and complex. I don't want Euler's identity. – Sawarnik Nov 18 '13 at 15:25
  • @Sawarnil, can have a look into http://math.stackexchange.com/questions/470614/find-the-value-of-textrmcosec2-left-frac-pi7-right-textrmcosec2-left and http://math.stackexchange.com/questions/544228/is-sum-k-1m-1-frac1-sin2-frack-pim-fracm2-13-true-for-m?lq=1 – lab bhattacharjee Nov 19 '13 at 04:39

3 Answers3

2

Let $7\theta=\pi, 4\theta=\pi-3\theta\implies \sin4\theta=\sin(\pi-3\theta)=\sin3\theta$

$$\frac1{\sin3\theta}+\frac1{\sin2\theta}$$

$$=\frac1{\sin4\theta}+\frac1{\sin2\theta}$$

$$=\frac{\sin4\theta+\sin2\theta}{\sin4\theta\sin2\theta}$$

$$=\frac{2\sin3\theta\cos\theta}{\sin4\theta\sin2\theta}\text{ Using } \sin2C+\sin2D=2\sin(C+D)\cos(C-D)$$

$$=\frac{2\cos\theta}{2\sin\theta\cos\theta}$$

$$=\frac1{\sin\theta}$$

All cancellations are legal as $\sin r\theta\ne0$ for $7\not\mid r$

lab bhattacharjee
  • 274,582
  • FIne! I missed the tricked that $\sin (\pi-\theta)=\sin\theta$ in my answer. – Sawarnik Nov 18 '13 at 15:28
  • 1
    @Sawarnik, here are some links of questions, please don't look into before honest try from your end (the numbers from your link : http://ohkawa.cc.it-hiroshima.ac.jp/AoPS.pdf/Trigonometry%20Problems%20-%20Amir%20Hossein%20Parvardi.pdf) : 7--http://math.stackexchange.com/questions/503575/solving-a-trigonometric-equation 20-- Related : http://math.stackexchange.com/questions/425966/finite-series-reciprocals-of-sines 14--http://math.stackexchange.com/questions/265229/prove-that-cot2-pi-7-cot22-pi-7-cot23-pi-7-5 34--http://math.stackexchange.com/questions/557360/a-trigonometric-equation – lab bhattacharjee Nov 18 '13 at 15:52
  • 42-- Related : http://math.stackexchange.com/questions/17966/how-can-we-sum-up-sin-and-cos-series-when-the-angles-are-in-arithmetic-pro 45--http://math.stackexchange.com/questions/346368/sum-of-tangent-functions-where-arguments-are-in-specific-arithmetic-series – lab bhattacharjee Nov 18 '13 at 15:52
2

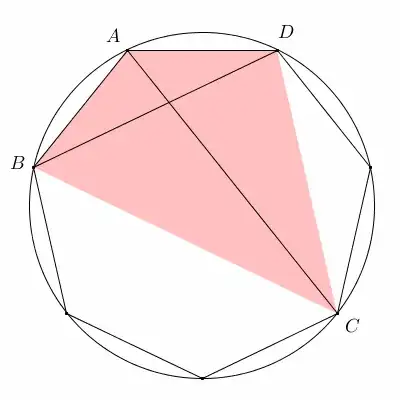
enter image description here

consider regular 7-gon. applying Ptolemy theorem for $\square ABCD$,
we get $BD\cdot AC=AB\cdot CD+AD\cdot BC$
$BC=AC=2R\sin\dfrac{3\pi}{7}$ , $~BD=CD=2R\sin\dfrac{2\pi}{7}$ , $~AB=AD=2R\sin\dfrac{\pi}{7}$
we're done, where $R$ is the circumradius of regular 7-gon.

chloe_shi
  • 2,855
1

Let $7\theta=\pi$

$$\frac1{\sin3\theta}+\frac1{\sin2\theta}-\frac1{\sin\theta}$$

$$=\frac{2\sin2\theta\sin\theta+2\sin3\theta\sin\theta-2\sin2\theta\sin3\theta}{2\sin3\theta\sin2\theta\sin\theta}$$

Now use $\displaystyle2\sin A\sin B=\cos(A-B)-\cos(A+B)$

and as $\displaystyle\cos(\pi-x)=-\cos x, \cos(7-r)\theta=\cos(7\theta-r\theta)=\cos(\pi-r\theta)=-\cos r\theta$

lab bhattacharjee
  • 274,582