A point $P$ is chosen $0.5$ units away from the centre of a circle of diameter $2$. Now two points are chosen randomly on the circumference of the circle. What is the probability that the triangle formed by those two points and point $P$ encloses the centre of the circle?
Asked
Active
Viewed 699 times
2
-
My insights are, this problem is equaivalento to finding two points on different side of a semicircle. Hence Probability is 0.5 – user106448 Nov 17 '13 at 07:16
-
2This is one of the many similar questions that answered this problem. – achille hui Nov 17 '13 at 07:53
1 Answers
1
The probability is $\frac14$.
As achille hui says in comments from the question, this is the probabilty that a triangle whose vertices are uniformly and independently distributed on the unit circle contains the origin. This probability is computed in the given link, but we have to explain why this is the same.
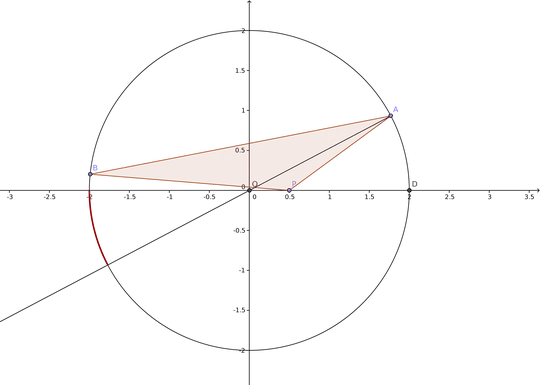
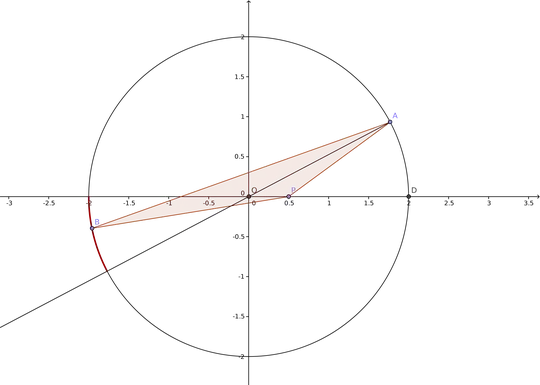
First consider an apparently more general problem where we don't know the abscissa of $P$. We only know that $P$ has coordinate $(x,0)$ (with $0<x\leq\text{radius of the circle}$).
Let's call $A$ and $B$ the two random points. By symmetry we can assume that $A$ is in the upper half. The triangle $ABP$ contains the origin if and only if $B$ is in the arc starting from $(-1,0)$ and ending at $-A$ (going anticlockwise).
This is independent from $x$, so we could consider that $P$ is the point $(1,0)$ and since the uniform distribution is rotation invariant we can consider that the $P$ is also a random point on the circle.
Gilles Bonnet
- 2,043