Finding the fixed point and the suitable range

Question

I have to find the fixed point of x$^3$-x$^2$-1=0.Then x=(1/x$^2$)+1 where I chose g(x)=(1/x$^2$)+1 .Then I tried to find a fixed point for g(x).Since I don't know the range of x,I chose x$\in$[1.3,1.6] as the suitable range because in this range 1.3

My question is my chosen range a suitable one? I wrote a python program to find the fixed point and it found the fixed point 1.47 in just 13 iterations.Why do I get from the program 13 and from calculation 62?

def fixedPoint(f,epsilon):

    guess=1.3
    count=0
    p=f(guess)


    while abs(p- guess)>=epsilon:

        guess=p
        p=f(guess)
        count+=1
        print guess

    return "The fixed point is "+str(round(guess,2))+"  and it took "+str(count)+" iterations"

def f(x):

    k=(1/x**2)+1
    return k

Answer 1

We have:

$$x = g(x) = \dfrac{1}{x^2} +1$$

By the way, we could just as well choose a different $g(x)$ and some can be better than others.

If we plot this, it shows:

For a starting value of $x=1.3$, the fixed point should result in:

$$x = 1.46557137542.$$

As to when it works, see these Fixed Point Iteration notes, but here is a summary:

• Let $\alpha$ be the root of the equation $x = g(x)$.
• The iteration is $x_{n+1} = g(x_n)$.
• We can derive that $(x_{n+1} - \alpha) \approx g'(\alpha)(x_n - \alpha)$
• The iteration converges if $|g'(\alpha)| < 1$, and diverges if $|g'(\alpha)|>1$.
• The rare case $g(\alpha)=1$ can correspond either to very slow convergence or to very slow divergence.
• See Thm. 9.4 in the notes.
• See How to find the interval $[a,b]$ on which fixed-point iteration will converge of a given function $f(x)$? for guidance on what that range is.

Answer 2

You used an upper bound on the absolute value of the derivative to find an upper bound on the number of iterations required for the desired precision.

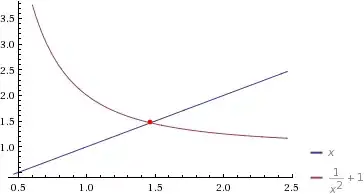
The Mean Value Theorem says that if $x_n$ is the $n$-th estimate, and $r$ is the root, then $|x_{n+1}-r|$ is equal to $|x_n-r|$ times the absolute value of $g'(x)$ somewhere between $x_n$ and $r$.

It is true that the derivative has absolute value $\lt \frac{2}{(1.3)^3}$. But that only gives us an upper bound on the "next" error in terms of the previous error.

Furthermore, as $x_n$ gets close to $r$, say around $1.4$ or closer, the relevant derivative has significantly smaller absolute value than your $k$.

A further huge factor in this case is that the derivative is negative. That means that estimates alternate between being too small and being too big. When $x_n\gt r$, the derivative has significantly smaller absolute value than your estimate $k$.

Even at the beginning, the convergence rate is faster than the one predicted from the pessimistic estimate of the derivative, particularly since half the time $x_n\gt r$. After a while, the disparity, for $x_n\lt r$, gets greater.

Remark: You know the root $r$ to high precision. It might be informative to modify the program so that at each stage it prints out $\frac{x_{n+1}-r}{x_n-r}$. That way, you can make a comparison between the upper bound $\frac{2}{(1.3)^3}$ on the ratio, and the actual ratio. Even not very large differences, under repeated compounding, can result in much quicker convergence than the one predicted from the upper bound.