Is it a coincidence that $\Re\ e^{\frac{1}{2} +i\rho_1}$ and $\ \zeta^{\frac{1}{2} +i\rho_1}$ are so close in value?
From Mathematica I am getting $e^{\frac{1}{2} +i\rho_1} \approx 1.05148\times10^{-6}.$
Is it a coincidence that $\Re\ e^{\frac{1}{2} +i\rho_1}$ and $\ \zeta^{\frac{1}{2} +i\rho_1}$ are so close in value?

From Mathematica I am getting $e^{\frac{1}{2} +i\rho_1} \approx 1.05148\times10^{-6}.$
I'm going to assume that you by $\rho_1$ mean the imaginary part of the first non-trivial zero of $\zeta(s)$ and that you by $\zeta^{\frac12+i\rho_1}$ mean $\zeta\left(\frac12+i\rho_1\right)$, which obviously equals $0$ if my first assumption is correct.
Your question can then be rephrased as "Is it a coincidence that $\Re\;e^{\frac12+i\rho_1}$ is very close to $0$?"
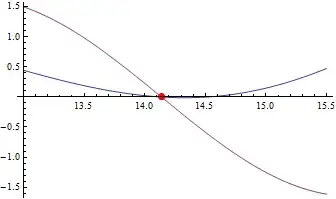
First note that $e^{\frac12+i\rho_1} = e^{\frac12}\left(\cos \rho_1 + i\sin \rho_1\right)$ and thus $\Re\; e^{\frac12+i\rho_1} = \sqrt{e}\cos\rho_1$.
Since $\cos x = 0$ is true for $x = \left(n + \frac12\right)\pi, \;n \in \Bbb{Z}$, your observation is true if $\rho_1$ is in some sense close to $\left(n+\frac12\right)\pi$. And indeed, $\frac{\rho_1}{\pi} \approx 4.49922$. Your question can therefore again be rephrased to:
"Is it a coincidence that $\rho_1$ is close to $4.5\pi$?"
I believe the answer to this is yes.
A related question, which includes your observation and more discussions about how $\rho_1$ can be approximated, can be found here.