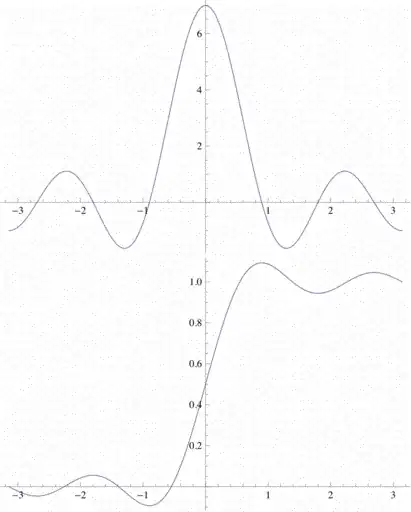
Plotting the series $$\displaystyle y = \sum_{k} \frac{\sin kx }{k}$$
In the limit it would look like
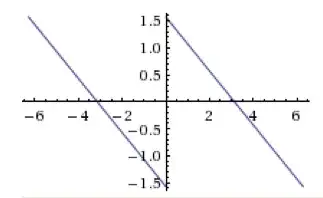
Taking a finite number of terms, I want to understand what is the reason for the jiggling at the extremes, while there the jiggling in the middle is so small its not noticable.
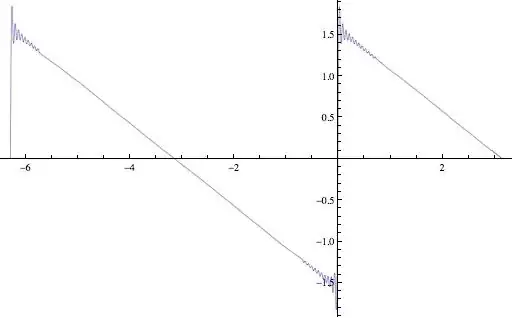
I truncated the sum to $1,2,3\; \mbox{and}\;4$ terms but cannot deduce much of a reason.

The "jiggling" was noticeable here because the sum is linear in the limit, however, for an expression like $$p(x) = x\prod_k\Big(1-\frac{x^2}{k^2\pi^2}\Big) $$
Does the truncated expression oscillate back and forth the limit?