Can we simplify $\int_{0}^{\infty}\frac{{\sin}^px}{x^q}dx$?

Question

We know the followings : $$\int_{0}^{\infty}\frac{{\sin}x}{x}dx=\int_{0}^{\infty}\frac{{\sin}^2x}{x^2}dx=\frac{\pi}{2},\int_{0}^{\infty}\frac{{\sin}^3x}{x^3}dx=\frac{3\pi}{8}.$$ Also, we can get $$\int_{0}^{\infty}\frac{{\sin}^3x}{x^2}dx=\frac{3\log 3}{4},\int_{0}^{\infty}\frac{{\sin}^4x}{x^3}dx=\log 2.$$ Then, I got interested in their generalization.

Question : Letting $p,q\in\mathbb N$, can we simplify the following? $$\int_{0}^{\infty}\frac{{\sin}^px}{x^q}dx$$

I don't have any good idea. Could you show me how to simplify this?

Update : I crossposted to MO.

Answer 1

The formulas you seek are \begin{align*} \int_0^\infty {\sin^p x\over x^q}\,dx & = \left\{\begin{array}{ll} \displaystyle{(-1)^{(p+q)/2}\pi\over 2^{p+1}(q-1)!}\sum_{k = 0}^p(-1)^k{p\choose k} |p - 2k|^{q-1} & \text{$p,q$ even,} \\[2em] \displaystyle {(-1)^{(p+q)/2-1}\pi\over 2^{p+1}(q-1)!}\sum_{k = 0}^p (-1)^k{p\choose k} \operatorname{sign}(p-2k) |p-2k|^{q-1} & \text{$p,q$ odd,} \\[2em] \displaystyle {(-1)^{(p+q+1)/2} \over 2^p (q-1)!} \sum_{k = 0\atop k\not = p/2}^p (-1)^k {p\choose k} |p-2k|^{q-1}\log{|p - 2k|} & \text{$p$ even, $q$ odd,} \\[2em] \displaystyle {(-1)^{(p+q-1)/2} \over 2^p (q-1)!} \sum_{k = 0\atop k\not = (p\pm1)/2}^p (-1)^k {p\choose k} \operatorname{sign}(p-2k) |p-2k|^{q-1}\log{|p - 2k|} & \text{$p$ odd, $q$ even,} \end{array}\right. \end{align*}

---

Here's the basic idea behind my proof (the idea grew out of this old answer): Find the Fourier transform of the function $\mathbb 1_{(0,\infty)}(x) \sin^q{x}/x^p$ and evaluate it at zero. Finding that Fourier transform is of course the hard part. The basic idea is to look at the Fourier transform of the generalized function $\mathbb 1_{(0,\infty)} |x|^{-s}$, where $s$ is a continuous variable.

---

When $s\notin\mathbb N$, the function $u_s(x) = \mathbb 1_{(0,\infty)}(x)|x|^{-s}$ can be made into a tempered distribution on the real line in a rigorous way (see Chapter 3 of Gelfand & Shilov's Generalized Functions for instance, or this Wikipedia page). Here $\mathbb 1_{(0,\infty)}$ is the characteristic function of the interval $(0,\infty)$. The Fourier transform of $u_s$ is \begin{align*} \hat{u}_s(t) & = \Gamma(1-s)\sin{\left({\pi s\over 2}\right)} |t|^{s-1} - i \Gamma(1-s) \cos{\left({\pi s\over 2}\right)} \operatorname{sign}(t) |t|^{s-1} \\ & = {\pi\over 2\Gamma(s)\cos{\left({\pi s\over 2}\right)}} |t|^{s-1} - { i\pi\over 2\Gamma(s)\sin{\left({\pi s\over 2}\right)}} \operatorname{sign}(t) |t|^{s-1}; \end{align*} See here, on the entry for $|x|^\alpha$, for instance. I used the reflection formula to pass from the first line to the second (because the second form is more convenient for us but the first follows more easily from this Wikipedia entry). It follows that for $s\notin \mathbb N$ the Fourier transform of $\sin^p{(x)} u_s(x) = \mathbb 1_{(0,\infty)}(x)|x|^{-s}\sin^p{(x)}$ is \begin{align*} \mathcal F(\sin^p{(x)} u_s(x))(t) & = {1\over (2i)^p}\sum_{k = 0}^p (-1)^k{p\choose k} \mathcal F(e^{i(p-2k)x}u_s(x)) \\ & = {\pi\over 2^{p+1}i^p\Gamma(s)\cos{\left({\pi s\over 2}\right)}}\sum_{k = 0}^p(-1)^k{p\choose k} |t - p + 2k|^{s-1} \\ & \quad -{\pi\over 2^{p+1}i^{p-1}\Gamma(s)\sin{\left({\pi s\over 2}\right)}}\sum_{k = 0}^p (-1)^k{p\choose k} \operatorname{sign}(t-p+2k) |t-p+2k|^{s-1}. \end{align*} Thus for $0 < s \leq p$ and $s\notin \mathbb N$, we get \begin{align*} \int_0^\infty{\sin^p x\over x^s}\,dx & = \mathcal F(\sin^p{(x)} u_s(x))(0) \\ & = {\pi\over 2^{p+1}i^p\Gamma(s)\cos{\left({\pi s\over 2}\right)}}\sum_{k = 0}^p(-1)^k{p\choose k} |p - 2k|^{s-1} \\ & \quad + {\pi\over 2^{p+1}i^{p-1}\Gamma(s)\sin{\left({\pi s\over 2}\right)}}\sum_{k = 0}^p (-1)^k{p\choose k} \operatorname{sign}(p-2k) |p-2k|^{s-1}. \end{align*} Actually, when $p$ is even only the first sum on the right-hand side will survive, and when $p$ is odd only the second sum will survive. This is true because if one breaks $u_s$ up into even and odd components ($u_s(x) = |x|^{-s}/2 + \operatorname{sign}(x)|x|^{-s}/2$), then the first sum is the integral over the real line of the even part multiplied by $\sin^p{x}$ while the second sum is the integral of the odd part multiplied by $\sin^p{x}$. So what we really have is \begin{align*} \int_0^\infty{\sin^p x\over x^s}\,dx &= \left\{ \begin{array}{ll} \displaystyle{\pi\over 2^{p+1}i^p\Gamma(s)\cos{\left({\pi s\over 2}\right)}}\sum_{k = 0}^p(-1)^k{p\choose k} |p - 2k|^{s-1} & \text{$p$ even,} \\[2em] \displaystyle {\pi\over 2^{p+1}i^{p-1}\Gamma(s)\sin{\left({\pi s\over 2}\right)}}\sum_{k = 0}^p (-1)^k{p\choose k} \operatorname{sign}(p-2k) |p-2k|^{s-1} & \text{$p$ odd}. \end{array}\right. \tag{1} \end{align*}

The above formulas clearly give the desired result when $s \in \mathbb N$ has the same parity as $p$ (and of course is no greater than $p$), and then they simplify to the formulas I gave at the beginning of this answer. So it remains only to think about what happens when either $p$ is even and $s$ is odd or $p$ is odd and $s$ is even. Both cases are similar; we simply take a limit. As it turns out, $\sum (-1)^k {p\choose k} |p - 2k|^{s-1}$ vanishes when $p$ is even and $s$ odd, and likewise $\sum (-1)^k{m\choose k} \operatorname{sign}(p-2k) |p-2k|^{s-1}$ vanishes when $p$ is odd and $s$ even (provided in both cases that $0<s< p$). The zeros of these sums cancel against the zeros of the sine and cosine terms that appear in the denominators. This assertions must be true, because both sides of the formula $(1)$ are continuous functions of the variable $s$ and the left hand side is finite when $s\leq p$ is a positive integer with parity opposite that of $p$. Finally, to arrive at the formulas given in the beginning, simply apply l'Hopital's rule. Thus, for instance, when $p$ is even and $q$ is odd, \begin{align*} \lim_{s\to q} {1\over \cos{\left({\pi s\over 2}\right)}}&\sum_{k = 0}^p(-1)^k{p\choose k} |p - 2k|^{s-1} \\ & = (-1)^{(q+1)/2}{2\over \pi} \sum_{k = 0\atop k\not = p/2}^p (-1)^k{p\choose k} |p - 2k|^{q-1} \log{|p-2k|}, \end{align*} and the rest follows easily.

Answer 2

Let's consider $$I(k,q)=\int_0^\infty\frac{\sin^k(x)}{x^q}dx$$ where $k$ is positive integer and $q$ is rational (not necessarily an integer).

Using the formula $\frac{1}{x^q}=\frac{1}{\Gamma(q)}\int_0^\infty{t}^{q-1}e^{-xt}dt$

we get $I(k,q)=\frac{1}{\Gamma(q)}\int_0^\infty{t}^{q-1}dt\int_0^\infty\sin^k(x){e}^{-xt}dx$, where $\Gamma(x)$ is Gamma-function.

Integrating by part and grouping the terms with the same power of $\sin(x)$ we can get that

$$I(k,q)=\frac{k!}{\Gamma(q)}\int_0^{\infty}\frac{t^{q-2}}{(t^2+2^2)(t^2+4^2)...(t^2+k^2)}dt, k=2n, q>1, n=1, 2,3...$$

$$I(k,q)=\frac{k!}{\Gamma(q)}\int_0^{\infty}\frac{t^{q-1}}{(t^2+1^2)(t^2+3^2)...(t^2+k^2)}dt, k=2n-1, q>0, n=1, 2,3...$$

To evaluate the integrals let's consider the following contour: along the cut from $0$ to ${\infty}$ (along the $X$ axis), big circle of radius $R$ (counter clockwise), along the other bank of the cut back to $0$ and along a small circle $r$ around $0$ (around a brunch point of $t^q$ - $q$ is rational) to the starting point.

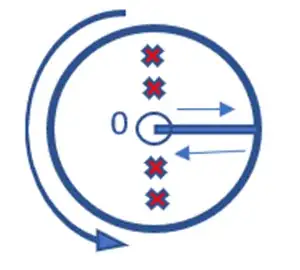
Making a full round in the positive direction, on the lower bank of the cut the integrand gets additional factor $e^{2\pi{iq}}$. Integral along this closed contour is equal to the sum of residuals in simple poles, and integrals along big and small circle set to zero as $R\to\infty$ and $r\to0$. So, $$I(k,q)(1-e^{2\pi{iq}})=2\pi{i}\frac{k!}{\Gamma(q)}\sum{Res}\frac{t^{q-2}}{(t^2+2^2)(t^2+4^2)...(t^2+k^2)}, k=2n$$ $$I(k,q)(1-e^{2\pi{iq}})=2\pi{i}\frac{k!}{\Gamma(q)}\sum{Res}\frac{t^{q-1}}{(t^2+1^2)(t^2+3^2)...(t^2+k^2)}, k=2n-1$$ Finally, for even ($k=2n$), $q>1$ ($q$ - rational); $a=2, b=4, ...=k$ $$I(k,q)=\frac{-\pi{k!}}{2\Gamma(q)\cos\frac{\pi{q}}{2}}\left(\frac{a^{q-3}}{(b^2-a^2)(c^2-a^2)..(k^2-a^2)}+\frac{b^{q-3}}{(a^2-b^2)(c^2-b^2)..(k^2-b^2)}+..\right)$$ Or, after slight further simplification, $$I(k,q)=\frac{-\pi{k!}2^{q-2n-2}}{\Gamma(q)\cos\frac{\pi{q}}{2}}\left(\frac{a^{q-3}}{(b^2-a^2)(c^2-a^2)..((\frac{k}{2})^2-a^2)}+\frac{b^{q-3}}{(a^2-b^2)(c^2-b^2)..((\frac{k}{2})^2-b^2)}+..\right)$$ where $a=1, b=2, c=3…=\frac{k}{2}(=n)$

For odd ($k=2n-1$), $q>0$, $a=1, b=3, ...=k$ $$I(k,q)=\frac{\pi{k!}}{2\Gamma(q)\sin\frac{\pi{q}}{2}}\left(\frac{a^{q-2}}{(b^2-a^2)(c^2-a^2)..(k^2-a^2)}+\frac{b^{q-2}}{(a^2-b^2)(c^2-b^2)..(k^2-b^2)}+..\right)$$

The formulas are practical for calculations, and any integral $I(k,q)=\int_0^\infty\frac{\sin^k(x)}{x^q}dx$ for not too big integer $k$ can easily be evaluated. Just few examples:

1. $I(k=4,q=2)=\int_0^\infty\frac{sin^4(x)}{x^2}dx$, $k=4$ ($k$ is even), and we have only $a=2, b=4$. Therefore, $$I(4,2)=-\frac{\pi{4!}}{2\Gamma(2)\cos\frac{\pi{2}}{2}}\left(\frac{2^{-1}}{(4^2-2^2)}+\frac{4^{-1}}{(2^2-4^2)}\right)=\frac{12\pi}{4^2-2^2}(\frac{1}{2}-\frac{1}{4})=\frac{\pi}{4}$$
2. $I(k=4,q=4)=\int_0^\infty\frac{\sin^4(x)}{x^4}dx=-\frac{4!\pi2^2}{2^4\Gamma(4)}\left(\frac{1}{2^2-1^2}+\frac{2}{1^2-2^2}\right)=-\frac{\pi}{3}(1-2)=\frac{\pi}{3}$
3. $I(k=3,q=\frac{1}{2})=\int_0^\infty\frac{\sin^3(x)}{\sqrt{x}}dx=\frac{6\pi\sqrt{2}}{2\sqrt{\pi}}\left(\frac{1^-\frac{3}{2}}{3^2-1^2}+\frac{3^-\frac{3}{2}}{1^2-3^2}\right)=-\frac{\sqrt\pi}{4\sqrt6}(3\sqrt3-1)$
4. $I(k=5,q=\frac{3}{2})=\int_0^\infty\frac{\sin^5(x)}{x^\frac{3}{2}}dx=\frac{5!\pi}{2\Gamma(\frac{3}{2})\sin\frac{3\pi}{4}}\left(\frac{1}{\sqrt1(3^2-1^2)(5^2-1^2)}+\frac{1}{\sqrt3(1^2-3^2)(5^2-3^2)}+\frac{1}{\sqrt5(1^2-5^2)(3^2-5^2)}\right)=\sqrt{\frac{5\pi}{2}}\frac{2\sqrt5-\sqrt15+1}{24}$
5. At some $q$ there are uncertainties (when $\cos\frac{\pi{q}}{2}$ or $\sin\frac{\pi{q}}{2}=0$ in the denominators) that need to be evaluated. For instance, $I(k=3,q=2)=\int_0^\infty\frac{\sin^3(x)}{x^2}dx$. We have $a=1, b=3$, we set $q=2+\epsilon$ and $$I(3,2)=\lim_{\epsilon\to0}\frac{6\pi}{2}\frac{1}{\sin\frac{\pi(2+\epsilon)}{2}}\left(\frac{1^\epsilon}{3^2-1^2}+\frac{3^\epsilon}{1^2-3^2}\right)=$$$$=-\lim_{\epsilon\to0}\frac{6}{\epsilon}\left(\frac{1^0}{3^2-1^2}+\frac{\epsilon\log(1)}{3^2-1^2}+\frac{3^0}{1^2-3^2}+\frac{\epsilon\log(3)}{1^2-3^2}\right)=\frac{3\log3}{4}$$