Why is $\sin(t)\cos(t)$ equal to $\frac{1}{2}\sin(2t)$?

Question

I know that $\sin(t)\cos(t)$ is equal to $\frac{1}{2}\sin(2t)$ but I do not understand why, please explain it to me!

This question has some explanations "from the first principles". — Dan Shved, Nov 08 '13 at 10:29

subroy13 · Answer 1 · 2023-08-25T03:59:23.247

3

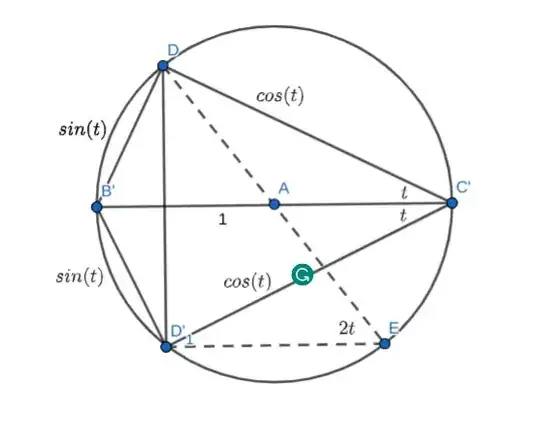
A visual proof by applying Ptolemy's Theorem.

Imagine the circle as shown with diameter $1$. Then, by applying Ptolemy's theorem on the cyclic quadrilateral $B'DC'D'$ we have $B'D \times C'D' + C'D \times B'D' = B'C' + DD'$, equaling $2 \sin(t)\cos(t) = \sin(2t)$. To see why $D'D = \sin(2t)$, notice the triangle $D'DE$.

edited Aug 25 '23 at 03:59

answered Jul 16 '23 at 13:56

subroy13

51

score 3 · Accepted Answer · answered Nov 08 '13 at 10:22

3

$\sin 2t =\sin (t+t)= \sin t \cos t+ \cos t\sin t =\ldots$.

answered Nov 08 '13 at 10:22

Boris Novikov

17,470

3

This is just solving a mystery by appealing to a bigger mystery ) – Dan Shved Nov 08 '13 at 10:23
Although who knows, maybe the problem was indeed in making this connection... – Dan Shved Nov 08 '13 at 10:24
@Dan Shved: Yes, I hope that if OP don't know $\sin(x+y)$, he will ask this. – Boris Novikov Nov 08 '13 at 10:27
This was actually a good answer, since I didn't thaugt about that formula. – rablentain Nov 08 '13 at 11:02

score 0 · Answer 3 · answered Aug 25 '23 at 07:25

Complex number solution $$ \cos t = \frac{e^{it}+e^{-it}}{2} \\ \sin t = \frac{e^{it}-e^{-it}}{2i} \\ \sin t\cos t = \frac{e^{it}-e^{-it}}{2i}\cdot\frac{e^{it}+e^{-it}}{2} = \frac{e^{i2t}-e^{-i2t}}{4i} = \frac12 \frac{e^{i2t}-e^{-i2t}}{2i} = \frac12 \sin(2t) $$

score 0 · Answer 4 · answered Aug 25 '23 at 07:45

Let $\triangle ABC$ be the isoceles triangle with sides $AB=AC=1$ and $\angle BAC=2t$. Let $AD$ be the altitude of the base side $BC$. Then the area of the triangle can be computed in two ways.

$(ABC)=\frac12 BC AD=\frac12 (2\sin t)\cos t=\sin t\cos t$

and

$(ABC)=\frac12AB\,AC\sin(\angle BAC)=\frac12\sin(2t).$

score 0 · Answer 5 · answered Aug 25 '23 at 08:04

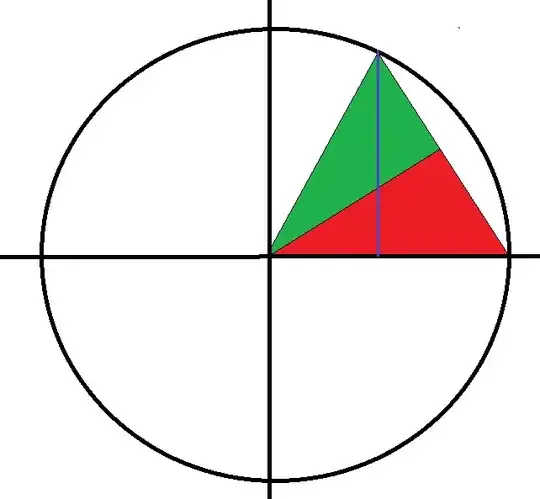
Lets suppose the larger triangle is an isoceles triangle with its vertex at the origin. The legs are of lenght 1 (and it has been inscribed in the unit circle). It has been bisected into two congruent right triangles.

We will say that the larger triangle has a vertex angle of $2t$, and each of the smaller triangles have a measure t at that vertex.

The lenght of the segment that bisects the isosceles triangle (the border between red and green) has lenght $\cos t$ each of the right triangles have legs of $\sin t$ opposite the angle.

The area of the each of these is then $\frac 12 \sin t\cos t$ and together their area is $\sin t\cos t$

The lenght of the blue line is $\sin 2t$ Using that as the height at $1$ as the base gives the area of the large tringle as $\frac 12 \sin 2t$

We have now calculated the same area by two different methods and they must be equal.

$\frac 12 \sin 2t = \sin t\cos t$

The area of the large triangle is $\frac 12 \sin t$

score -1 · Answer 6 · answered Nov 08 '13 at 10:54

-1

We now that: $$\sin(2t)=\frac{1}{2}\sin t\cos t/:\frac{1}{2}$$ Now we have: $$\frac{1}{2}\sin(2t)=\sin t\cos t$$

answered Nov 08 '13 at 10:54

Madrit Zhaku

5,294

Why is $\sin(t)\cos(t)$ equal to $\frac{1}{2}\sin(2t)$?

6 Answers6