2

I've having trouble understanding something in Turi's Category Theory Lecture Notes from The University of Edinburgh, which can be found here. It's the proof of Theorem 7.1, part (3).

Here's the statement of the theorem:

Given a functor $U:\mathbf{D}\to\mathbf{C}$, if for every object $A$ of $\mathbf{C}$ there exists a universal arrow $\eta _{A}: A\to UF_{A}$ from $A$ to $U$, then the following holds:

  1. The function $F$ from objects of $\mathbf{C}$ to objects of $\mathbf{D}$ extends, by universality, to a functor $$F:\mathbf{C}\to\mathbf{D}$$ in the opposite direction to $U$.

  2. The arrow $\eta _{A}$ is natural in $A$: $$\eta :Id\Rightarrow UF$$.

  3. For every object $Y$ of $\mathbf{D}$ there is a universal arrow $\varepsilon _{Y}:FUY\to Y$ from $F$ to $Y$ obtained by universality:

enter image description here

  1. The arrow $\varepsilon _{Y}$ is natural in $Y$: $$\varepsilon : FU\Rightarrow Id.$$

Here's some of the proof so far.

Remember that, by definition of universality, for every $A\in\mathbf{C}$ there is some $F_{A}\in\mathbf{C}$ and some $\eta _{A}:A\to UF_{A}=UFA$ such that for any $f: A\to UY$, there exists a unique $f^{\sharp}:FA\to Y$ such that $f=Uf^{\sharp}\circ\eta_{A}$. The proof of part (1) gives us that for any $h:A\to B$ there exists a unique $Fh:= (\eta_{B}\circ h)^{\sharp}: FA\to FB$.

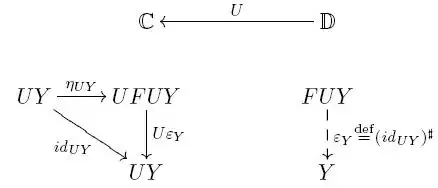
For any $Y\in\mathbf{D}$, universality then gives us a unique $\varepsilon_{Y}:=(id_{UY})^{\sharp}: FUY\to Y$ such that $id_{UY}=U\varepsilon_{Y}\circ\eta_{UY}$. [Think of putting $A=UY$ for just for a moment.]

In order to show that $\varepsilon_{Y}$ is a universal arrow from $F$ to $Y$, we need to show that for any $g:FA\to Y$, there exists a unique $g^{\flat }:A\to UY$ such that $g=\varepsilon_{Y}\circ Fg^{\flat }$.

For any such $g$ define $$g^{\flat}:=A\stackrel{\eta_{A}}{\longrightarrow}UFA\stackrel{Ug}{\longrightarrow}UY$$.

I've proven that, indeed, $$g=(g^{\flat})^{\sharp}$$ but I don't understand why $$(g^{\flat})^{\sharp}=\varepsilon_{Y}\circ Fg^{\flat}$$ follows from the naturality of $\eta$.

I think I'm nearly there with this overworked diagram

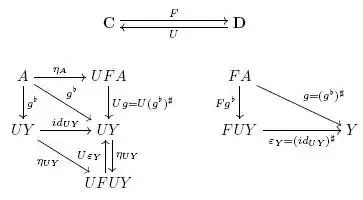
enter image description here

but I just don't see it yet. I can't prove it to myself. Please help. Is there something really subtle yet easy I've missed?

Thank you in advance.

[NB: The notes are about to introduce adjunctions via universal arrows so I want to play along (i.e. stick to what's given so far).]

Giorgio Mossa
  • 18,150
Shaun
  • 44,997

1 Answers1

1

Actually the proof follows from a combo of naturality of the $\eta_A$'s and their universal property.

From naturality we get the commutativity of the following diagram $$\require{AMScd}\begin{CD}A @>\eta_A>> UF(A) \\ @V{g^\flat}VV @V{UF(g^\flat)}VV\\ U(Y) @>{\eta_{U(Y)}}>> UFU(Y)\end{CD}$$ and composing on the left with $U(\epsilon_Y)$ we get that $$g^\flat = U(\epsilon_Y)\circ \eta_{U(Y)} \circ g^\flat = U(\epsilon_Y \circ F(g^\flat))\circ \eta_A$$ where the first equality follows the construction of $\epsilon_Y$.

From this equality we end up with the commutative square $$\begin{CD}A @>\eta_A>> UF(A) \\ @V\eta_AVV @VVU(\epsilon_Y \circ F(g^\flat))V \\ UF(A) @>U(g)>> U(Y)\end{CD}$$ and the from the universal property of $\eta_A$ it follows that $g=\epsilon_Y \circ F(g^\flat)$.

Since $g=(g^\flat)^\sharp$ it follows that $(g^\flat)^\sharp = \epsilon_Y \circ F(g^\flat)$.

Giorgio Mossa
  • 18,150
  • The solution I found was only slightly different: I made use of $id_{UY}=U\varepsilon_{Y}\circ\eta_{UY}$ and the uniqueness condition on $(g^{\flat})^{\sharp}$. However, I think yours is better. Thank you! – Shaun Nov 08 '13 at 16:09
  • 1
    @Shaun you're welcome. – Giorgio Mossa Nov 08 '13 at 16:10
  • It says I have to wait 18 hours until I can give you the bounty :/ – Shaun Nov 08 '13 at 16:10