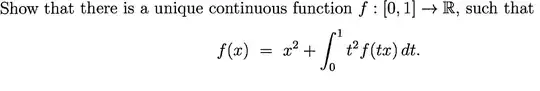
I have no idea where to even start, i have never dealt with question like this before, any direction you can give me would be greatly appreciated.
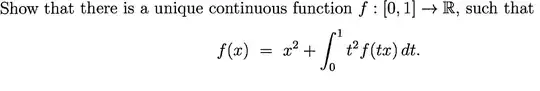
I have no idea where to even start, i have never dealt with question like this before, any direction you can give me would be greatly appreciated.
Hint: Consider the operator
$$T \colon C([0,1]) \to C([0,1]);\quad T(f) \colon x \mapsto x^2 + \int_0^1 t^2f(tx)\,dt.$$
Show that this operator satisfies the hypotheses of Banach's fixed point theorem.
|T(f)-T(g)|= int(t^2(f(tx)-g(tx))
is that ok so far?\
– greg Nov 03 '13 at 20:30