Evaluating the Integral: $\int_0^\infty \frac{( \frac{1}{2} - \cos x )}{x} dx$

Question

Evaluating the Integral: $\int_0^\infty\left[\frac{1}{2} - \cos\left(x\right)\right]\,{\rm dx \over x}$

I came upon this limit: $\lim_{x\rightarrow\infty} -Ci(x) + Ci(1/x) +\ln(x)$, is it $\gamma$ ?

Here $ Ci(x) = \gamma + \ln x + \int_0^x \frac{\cos t -1}{t} dt $ is the cosine integral and $\gamma$ is the Euler constant. The Limit and the Integral appear to be equal.

Answer 1

$$\int_0^{+\infty}\left(\frac 1 2 - \cos x\right)\frac {dx} x = \gamma$$

\begin{align*}\int_{1/n}^n \left(\frac 1 2 - \cos x\right)\frac {dx} x &= \int_{1/n}^1 \left(1 - \cos x\right)\frac {dx} x -\int_1^n \cos x\frac {dx} x+ \frac 1 2 \left(\int_1^n \frac {dx} x -\int_{1/n}^1 \frac {dx} x\right) \\ &=\int_{1/n}^1 (1-\cos x) \frac {dx} x - \int_1^n \cos x \frac {dx} x \end{align*} $$\bbox[0.2ex,border:0.5pt solid black]{\int_0^1 \frac {1-\cos(y)}y\,dy -\int_1^{+\infty} \frac {\cos(y)} y\,dy=\gamma}$$

Here is the proof of Gronwall, 1918. For $n$ a positive integer $$\begin{align} A(n) &= \int_0^{n\pi} \frac{1-\cos (y)}{y} dy - \ln ( n\pi ) \\ &= \int_0^1 \frac{1-\cos (y)}{y} dy + \int_1^{n\pi} \frac{1-\cos (y)}{y} dy - \ln ( n\pi ) \\ &= \int_0^1 \frac{1-\cos(y)}{t} dy - \int_1^{n\pi} \frac{\cos(y)}{y} dy \end{align}$$

With a change of variable $x = 2 \pi ny$:

$$\begin{align} \int_0^{n\pi} \frac{1-\cos(x)}{x} xy &= \int_0^{\frac{1}{2}} \frac{1 - \cos (2\pi ny)}{y} dy \\ &= \pi \int_0^{\frac{1}{2}} \frac{1 - \cos (2 \pi ny)}{\sin(\pi y)} dy + \int_0^{\frac{1}{2}} g(y) dy - \int_0^{\frac{1}{2}} g(y) \cos ( 2 \pi ny) dy \end{align}$$

$g(y) = \frac{1}{y} - \frac{\pi}{\sin (\pi y)}$ which is continuous on $[0,\frac{1}{2}]$ with $g(0) = 0$.

With Riemann-Lebesgue theorem $$\int_0^\frac{1}{2} g(y) \cos ( 2 \pi n y ) dy \rightarrow 0 \text{ for } n \rightarrow + \infty$$

$$\begin{align} \int_0^\frac12 g(y) dy &= \lim_{s \to 0^+} \int_s^\frac12 \left( \frac 1y - \frac \pi{\sin(\pi y)} \right) dy \\ &= \lim_{s \to 0^+} \left[ \ln \left( \frac{y}{\tan ( \pi/2\;y )} \right) \right]_s^{\frac{1}{2}} = \ln ( \pi ) - 2 \ln (2) \end{align}$$

On the other hand $$\begin{align} \pi \int_{0}^{\frac{1}{2}} \frac{1 - \cos ( 2 \pi n y)}{\sin ( \pi y )} dy &= 2\pi \int_{0}^{\frac{1}{2}} \sum_{k=1}^{n} \sin ( (2k-1) \pi y ) dy \\ &= \sum_{k=1}^{n} \frac{2}{2k-1} ={\ln (n) + 2 \ln (2) + \gamma + o(1)} \end{align}$$

Finally $$A(n) = \gamma + o(1)$$

Thanks very much to Sladjan Stankovik for providing insight into this problem for me.

Answer 2

$\newcommand{\+}{^{\dagger}} \newcommand{\angles}[1]{\left\langle\, #1 \,\right\rangle} \newcommand{\braces}[1]{\left\lbrace\, #1 \,\right\rbrace} \newcommand{\bracks}[1]{\left\lbrack\, #1 \,\right\rbrack} \newcommand{\ceil}[1]{\,\left\lceil\, #1 \,\right\rceil\,} \newcommand{\dd}{{\rm d}} \newcommand{\down}{\downarrow} \newcommand{\ds}[1]{\displaystyle{#1}} \newcommand{\expo}[1]{\,{\rm e}^{#1}\,} \newcommand{\fermi}{\,{\rm f}} \newcommand{\floor}[1]{\,\left\lfloor #1 \right\rfloor\,} \newcommand{\half}{{1 \over 2}} \newcommand{\ic}{{\rm i}} \newcommand{\iff}{\Longleftrightarrow} \newcommand{\imp}{\Longrightarrow} \newcommand{\isdiv}{\,\left.\right\vert\,} \newcommand{\ket}[1]{\left\vert #1\right\rangle} \newcommand{\ol}[1]{\overline{#1}} \newcommand{\pars}[1]{\left(\, #1 \,\right)} \newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}} \newcommand{\pp}{{\cal P}} \newcommand{\root}[2][]{\,\sqrt[#1]{\vphantom{\large A}\,#2\,}\,} \newcommand{\sech}{\,{\rm sech}} \newcommand{\sgn}{\,{\rm sgn}} \newcommand{\totald}[3][]{\frac{{\rm d}^{#1} #2}{{\rm d} #3^{#1}}} \newcommand{\ul}[1]{\underline{#1}} \newcommand{\verts}[1]{\left\vert\, #1 \,\right\vert} \newcommand{\wt}[1]{\widetilde{#1}}$ $\ds{\lim_{\epsilon \to 0^{+}}\,\int_{\epsilon}^{1/\epsilon} \bracks{\half - \cos\pars{x}}\,{\dd x \over x} = \gamma.\quad}$ $\ds{\quad\gamma}$ is the Euler-Mascheroni Constant.

\begin{align} &\color{#c00000}{ \lim_{\epsilon \to 0^{+}}\,\int_{\epsilon}^{1/\epsilon}\bracks{ \half - \cos\pars{x}}\,{\dd x \over x}} =\lim_{\epsilon \to 0^{+}}\,\bracks{-\int_{\epsilon}^{1/\epsilon}{ \cos\pars{x} - 1 \over x}\,\dd x - \half\int_{\epsilon}^{1/\epsilon} {\dd x \over x}} \\[3mm]&=\lim_{\epsilon \to 0^{+}}\,\braces{ -\bracks{{\rm Ci}\pars{1 \over \epsilon} - \ln\pars{1 \over \epsilon} - \gamma} + \bracks{{\rm Ci}\pars{\epsilon} - \ln\pars{\epsilon} - \gamma} -\half\ln\pars{1/\epsilon \over \epsilon}}\tag{1} \end{align} where $\ds{{\rm Ci}\pars{x}}$ is one of the Cosine Integral Functions.

Expression $\pars{1}$ can be rewritten as \begin{align} &\color{#c00000}{ \lim_{\epsilon \to 0^{+}}\,\int_{\epsilon}^{1/\epsilon}\bracks{ \half - \cos\pars{x}}\,{\dd x \over x}} =\gamma + \lim_{\epsilon \to 0^{+}}\, \braces{-{\rm Ci}\pars{1 \over \epsilon} + \bracks{{\rm Ci}\pars{\epsilon} - \ln\pars{\epsilon} - \gamma}}\tag{2} \end{align}

However $$ \lim_{\epsilon \to 0^{+}}\,{\rm Ci}\pars{1 \over \epsilon} = 0\,,\qquad \lim_{\epsilon \to 0^{+}}\,\,\bracks{ {\rm Ci}\pars{\epsilon} - \gamma - \ln\pars{\epsilon}} = 0 $$

such that $\pars{2}$ leads to $$\color{#00f}{\large \lim_{\epsilon \to 0^{+}}\int_{\epsilon}^{1/\epsilon}\bracks{ \half - \cos\pars{x}}\,{\dd x \over x} = \gamma} $$

Answer 3

$$ \begin{align} &\lim_{n\to\infty}\int_{1/n}^n\frac{\frac12-\cos(x)}x\,\mathrm{d}x\\ &=\lim_{n\to\infty}\left(\log(n)-\int_{1/n}^1\frac{\cos(x)}x\,\mathrm{d}x-\int_1^n\frac{\cos(x)}x\,\mathrm{d}x\right)\tag{1a}\\ &=\int_0^1\frac{1-\cos(x)}x\,\mathrm{d}x-\int_1^\infty\frac{\cos(x)}x\,\mathrm{d}x\tag{1b}\\ &=\int_0^1(1-\cos(x))\,\mathrm{d}\log(x)-\lim_{n\to\infty}\int_1^{(2n+1)\pi/2}\cos(x)\,\mathrm{d}\log(x)\tag{1c}\\ &=-\int_0^1\log(x)\sin(x)\,\mathrm{d}x-\lim_{n\to\infty}\int_1^{(2n+1)\pi/2}\log(x)\sin(x)\,\mathrm{d}x\tag{1d}\\ &=-\lim_{n\to\infty}\int_0^{(2n+1)\pi/2}\log(x)\sin(x)\,\mathrm{d}x\tag{1e}\\ &=-\frac1{2i}\lim_{n\to\infty}\left(\int_0^{(2n+1)\pi/2}\log(x)\,e^{ix}\,\mathrm{d}x-\int_0^{(2n+1)\pi/2}\log(x)\,e^{-ix}\,\mathrm{d}x\right)\tag{1f}\\ &=-\frac1{2i}\lim_{n\to\infty}\left(i\int_0^{\left(n+\frac12\right)\pi}\!\!\left(\log(x){+}\tfrac{i\pi}2\right)e^{-x}\,\mathrm{d}x+i\int_0^{\left(n+\frac12\right)\pi}\!\!\left(\log(x){-}\tfrac{i\pi}2\right)e^{-x}\,\mathrm{d}x\right)\tag{1g}\\ &=-\int_0^\infty\log(x)\,e^{-x}\,\mathrm{d}x\tag{1h}\\[6pt] &=\gamma\tag{1i} \end{align} $$ Explanation:
$\text{(1a)}$: break up the integral into pieces
$\text{(1b)}$: reassemble the pieces and evalate the limit
$\text{(1c)}$: write the right hand integral as a limit
$\phantom{\text{(1c):}}$ prepare to integrate by parts
$\text{(1d)}$: integrate by parts
$\text{(1e)}$: combine the integrals
$\text{(1f)}$: $\sin(x)=\frac{e^{ix}-e^{-ix}}{2i}$
$\text{(1g)}$: Cauchy's Integral Theorem
$\text{(1h)}$: evaluate the limits and combine the integrals
$\text{(1i)}$: apply this answer

---

Contour Integration for $\bf{(1g)}$

$\newcommand{\Re}{\operatorname{Re}}\newcommand{\Im}{\operatorname{Im}}$ Step $\text{(1g)}$ above looks like one that is often encountered in contour integration, where the integrand along the "arc at infinity" vanishes sufficiently in absolute value. However, the absolute value of the integrands along both of the arcs at infinity grows like $\log(\Re(z))e^{-|\!\Im(z)|}$. Fortunately, they have opposite signs and cancel to within an error of $O\!\left(\frac1n\right)$. This has the same effect as if the absolute value of the integrand had vanished sufficiently.

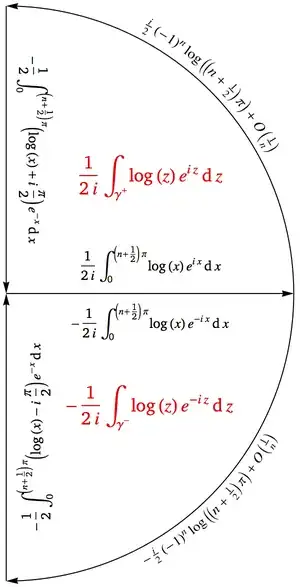
Integrating around the upper-right quadrant, we get the integral along the positive real axis by substituting $z=x$ and the integral along the positive imaginary axis by substituting $z=ix$.

The integral along the arc is a bit more complicated. As the integrand dies away like $e^{-y}$ as $y\to\infty$, we will compute the integral along $\left(n+\frac12\right)\pi+iy$, giving an error of $O\!\left(e^{-x}\right)$. $$ \begin{align} \frac1{2i}\int_{\left(n+\frac12\right)\pi}^{\left(n+\frac12\right)\pi+i\infty}\log(z)\,e^{iz}\,\mathrm{d}z &=\frac1{2}\int_0^\infty(\log(x)+\log(1+iy/x))\,e^{ix-y}\,\mathrm{d}y\tag{2a}\\ &=\frac{i}2(-1)^n\int_0^\infty\left(\log(x)+O(y/x)\right)e^{-y}\,\mathrm{d}y\tag{2b}\\[3pt] &=\frac{i}2(-1)^n\log\left(\left(n+\tfrac12\right)\pi\right)+O\!\left(\frac1n\right)\tag{2c} \end{align} $$ Explanation:
$\text{(2a)}$: use $z=x+iy$ where $x=\left(n+\frac12\right)\pi$
$\text{(2b)}$: $\log(1+iy/x)=O(y/x)$
$\text{(2c)}$: evaluate the integral

Integrating around the lower-right quadrant, we get the integral along the positive real axis by substituting $z=x$ and the integral along the negative imaginary axis by substituting $z=-ix$.

As the integrand dies away like $e^{-y}$ as $-y\to-\infty$, we will compute the integral along $\left(n+\frac12\right)\pi-iy$, giving an error of $O\!\left(e^{-x}\right)$. $$ \begin{align} -\frac1{2i}\int_{\left(n+\frac12\right)\pi}^{\left(n+\frac12\right)\pi-i\infty}\log(z)\,e^{-iz}\,\mathrm{d}z &=\frac1{2}\int_0^\infty(\log(x)+\log(1-iy/x))\,e^{-ix-y}\,\mathrm{d}y\tag{3a}\\ &=-\frac{i}2(-1)^n\int_0^\infty\left(\log(x)+O(y/x)\right)e^{-y}\,\mathrm{d}y\tag{3b}\\[3pt] &=-\frac{i}2(-1)^n\log\left(\left(n+\tfrac12\right)\pi\right)+O\!\left(\frac1n\right)\tag{3c} \end{align} $$ Explanation:
$\text{(3a)}$: use $z=x-iy$ where $x=\left(n+\frac12\right)\pi$
$\text{(3b)}$: $\log(1-iy/x)=O(y/x)$
$\text{(3c)}$: evaluate the integral

Thus, the sum of the integral along both arcs is $O\!\left(\frac1n\right)\to0$.