3

I'm interested in finding a non-piecewise approximation to a simple piecewise function.

$$ f(x) = \begin{cases} 0 & : x < T \\ x-T & : x \geq T \end{cases} $$

i.e. the function is $0$ until it is turned on at a certain point ($T$). And afterwards has a slope of $1$. $T$ is a parameter that can be arbitrarily varied.

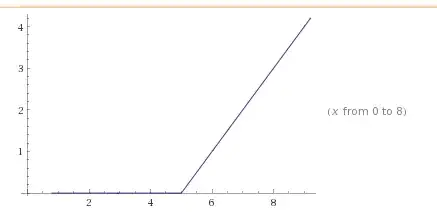
Here's a plot of the function for $T = 5$

Here's a plot of the function for T = 5

Michael Hardy
  • 1
ProverbialSun
  • 33
  • 1
    So, in other words, something along the lines of $\frac 12 (x-T)+|\frac 12(x-T)|$? If the function was $f:\mathbb Z^+\to \mathbb Z$ then there would be no need for absolutes even, but that is not the case... – abiessu Oct 25 '13 at 19:23
  • Sure...using an absolute value isn't really very different from a piecewise function though. Just calling it something different. – ProverbialSun Oct 25 '13 at 19:25
  • Okay, but I could also say $\sqrt{\frac 14 (x-T)^2}$ and note that I am taking the positive branch and suddenly I have a function without absolutes... – abiessu Oct 25 '13 at 19:28
  • 2
    After writing it using the absolute value you could replace $|\cdot|$ with something smooth as in this answer. – Antonio Vargas Oct 25 '13 at 19:28
  • Ah...the square root is a good trick. Thanks abiessu. I'll accept it as an answer if you'd care to write it that way. – ProverbialSun Oct 25 '13 at 19:44

2 Answers2

1

The function is equal to $f(x) = \dfrac{|x-5|+(x-5)}{2}.$

That could be considered "piecewise" because the absolute value function is defined piecewise, but its piecewise nature is not made explicit in this characterization.

If your function were defined only on a bounded interval I might think about a partial sum of a Fourier series.

PS: Alright, lets work with generalized functions and define derivatives accordingly Then $f'(x) = \left.\begin{cases} 1, & x>5, \\ 0, & x<5, \end{cases}\right\}$, and so $f''(x)=\delta(x-5)$.

Then the Fourier transform of $f''(x)$ is $$ (\mathcal F (f''))(t) = \int_{-\infty}^\infty e^{-itx} \delta(x-5)\,dx = e^{-5it}. $$ Recall that $$ (\mathcal F (f'))(t) = -it(\mathcal F f)(t), $$ so $$ (\mathcal F (f''))(t) = -t^2(\mathcal F f)(t). $$ So $$ (\mathcal F f)(t) = \frac{-e^{5it}}{t^2}. $$ Applying an inverse Fourier transform should return the original function. So you want an "approximation". Maybe I'd try doing the inverse Fourier transform but find only $\int_{-A}^{-\varepsilon}+\int_\varepsilon^A$ instead of $\int_{-\infty}^\infty$.

Michael Hardy
  • 1
1

To rewrite a function $f:\mathbb R\to \mathbb R$ which has absolute values as one which does not, use the square root of the square.

Given $f(x;T)=\frac 12 (x-T)+|\frac 12(x-T)|$, write

$$f(x;T)=\frac 12 (x-T)+\frac 12\sqrt{(x-T)^2}$$

To clarify for anyone reading this and thinking "why not just remove the square and the root?" make sure to note that only the positive branch of the square root is being used.

It should be possible to write a multi-branch function (e.g. "W") that operates this way, given the proper fractional components and overlaps.

abiessu
  • 8,115