How to find the center of an ellipse?

Question

I have the following data:-

• I have two points ($P_1$, $P_2$) that lie somewhere on the ellipse's circumference.
• I know the angle ($\alpha$) that the major-axis subtends on x-axis.
• I have both the radii ($a$ and $b$) of the ellipse.

I now need to find the center of this ellipse. It is known that we can get two possible ellipses using the above data.

I have tried solving this myself but the equation becomes so complex that I always give up.

This is what I have done till now:-

I took the normal ellipse equation $x^2/a^2 + y^2/b^2 = 1$. To compensate for the rotation and translation, I replaced $x$ and $y$ by $x\cos\alpha+y\sin\alpha-h$ and $-x\sin\alpha+y\cos\alpha-k$, respectively. $h$ and $k$ are x and y location of the ellipse's center.

Using these information I ended up with the following eq:- $$a B_1\pm\sqrt{a^2 B_1^2 - C_1(b^2 h^2 - 2 A_1 b^2 h)} = a B_2\pm\sqrt{a^2 B_2^2 - C_2 (b^2 h^2 - 2 A_2 b^2 h)} \quad (1)$$

where $A = x\cos\alpha +y\sin\alpha$, $B = -x\sin\alpha+y\cos\alpha$ and $C = a^2 B^2 + A^2 b^2 - a^2 b^2$.

Now the only thing I need to get is $h$ from (1). All other values are known, but I am not able to single that out.

Anyway if the above equations looks insane then please solve it yourself, your way. I could have drifted into some very complicated path.

Answer 1

Let the points be $P_1(x_1, y_1)$ and $P_2(x_2, y_2)$, assumed to lie on an ellipse of semiaxes $a$ and $b$ with the $a$ axis making angle $\alpha$ to the $x$ axis.

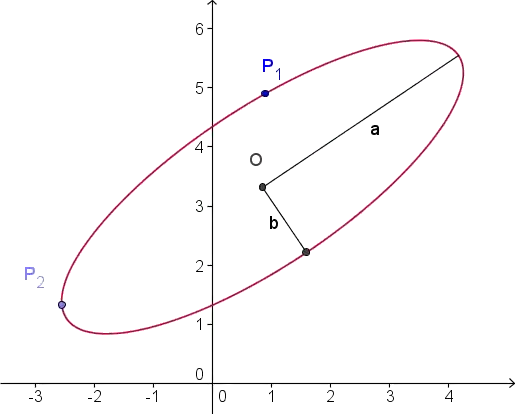
Following @joriki, we rotate the points $P_i$ by $-\alpha$ into points

$$Q_i(x_i \cos(\alpha) + y_i \sin(\alpha), y_i \cos(\alpha) - x_i \sin(\alpha)).$$

We then rescale them by $(1/a, 1/b)$ to the points

$$R_i(\frac{x_i \cos(\alpha) + y_i \sin(\alpha)}{a}, \frac{y_i \cos(\alpha) - x_i \sin(\alpha)}{b}).$$

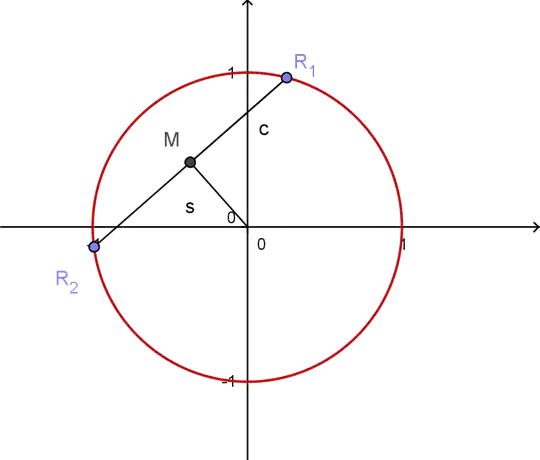
These operations convert the ellipse into a unit circle and the points form a chord of that circle. Let us now translate the midpoint of the chord to the origin: this is done by subtracting $(R_1 + R_2)/2$ (shown as $M$ in the figure) from each of $R_i$, giving points

$$S_1 = (R_1 - R_2)/2, \quad S_2 = (R_2 - R_1)/2 = -S_1$$

each of length $c$. Half the length of that chord is

$$c = ||(R_1 - R_2)||/2 = ||S_1|| = ||S_2||,$$

which by assumption lies between $0$ and $1$ inclusive. Set

$$s = \sqrt{1-c^2}.$$

The origin of the circle is found by rotating either of the $S_i$ by 90 degrees (in either direction) and rescaling by $s/c$, giving up to two valid solutions $O_1$ and $O_2$. (Rotation of a point $(u,v)$ by 90 degrees sends it either to $(-v,u)$ or $(v,-u)$.) For example, in the preceding figure it is evident that rotation $R_1$ by -90 degrees around $M$ and scaling it by $s/c$ will make it coincide with the circle's center. Reflecting the center about $M$ (which gives $2M$) produces the other possible solution.

Unwinding all this requires us to do the following to the $O_i$:

• Translate by $(R_1+R_2)/2$,
• Scale by $(a,b)$, and
• Rotate by $\alpha$.

The cases $c \gt 1$, $c = 1$, and $c=0$ have to be treated specially. The first gives no solution, the second a unique solution, and the third infinitely many.

FWIW, here's a Mathematica 7 function. The arguments p1 and p2 are length-2 lists of numbers (i.e., point coordinates) and the other arguments are numbers. It returns a list of the possible centers (or Null if there are infinitely many).

f[\[Alpha]_, a_, b_, p1_, p2_] := Module[
   {
    r, s, q1, q2, m, t, \[Gamma], u, r1, r2, x, v
    },
   (* Rotate to align the major axis with the x-axis. *)
   r = RotationTransform[-\[Alpha]];
   (* Rescale the ellipse to a unit circle. *)
   s = ScalingTransform[{1/a, 1/b}];
   {q1, q2} = s[r[#]] & /@ {p1, p2};
   (* Compute the half-length of the chord. *)
   \[Gamma] = Norm[q2 - q1]/2;
   (* Take care of special cases. *)
   If[\[Gamma] > 1, Return[{}]];
   If[\[Gamma] == 0, Return[Null]];
   If[\[Gamma] == 1, 
    Return[{InverseFunction[Composition[s, r]][(q1 + q2)/2]}]];
   (* Place the origin between the two points. *)
   t = TranslationTransform[-(q1 + q2)/2];
   (* This ends the transformations.  
   The next steps find the centers. *)
   (* Rotate the points 90 degrees. *)
   u = RotationTransform [\[Pi]/2];
   (* Rescale to obtain the possible centers. *)
   v = ScalingTransform[{1, 1} Sqrt[1 - \[Gamma]^2]/\[Gamma]];
   x = v[u[t[#]]] & /@ {q1, q2};
   (* Back-transform the solutions. *)
   InverseFunction[Composition[t, s, r]] /@ x
   ];

Answer 2

You can make your life a lot easier by rotating the two given points through $-\alpha$ instead of rotating the coordinate system through $\alpha$. Then you can work with the much simpler equation

$$\frac{(x-x_0)^2}{a^2}+\frac{(y-y_0)^2}{b^2}=1\;.$$

If you substitute your two (rotated) points $(x_1,y_1)$ and $(x_2,y_2)$, you get two equations for the two unknowns $x_0$,$y_0$. Subtracting these from each other eliminates the terms quadratic in the unknowns and yields the linear relationship

$$\frac{x_1^2-x_2^2-2(x_1-x_2)x_0}{a^2}+\frac{y_1^2-y_2^2-2(y_1-y_2)y_0}{b^2}=0\;.$$

You can solve this for one of the unknowns and substitute the result into one of the two quadratic equations, which then becomes a quadratic equation in the other unknown that you can solve.

Of course in the end you have to rotate the centre you find back to the original coordinate system.

Answer 3

Since the expression in whuber's comment was too darn long, here's the x-coordinate expression:

$$\begin{align*} &\frac1{2ab}\left(ab (x_1+x_2)+\left(a^2 (y_2-y_1)\cos^2\alpha+(a-b)(a+b) (x_1-x_2) \cos\,\alpha\sin\,\alpha+b^2 (y_2-y_1)\sin^2\alpha\right)\right.\\ &\left.\surd \left(\left(b^2 \left((x_1-x_2)^2+(y_1-y_2)^2\right)+a^2 \left(-8 b^2+(x_1-x_2)^2+(y_1-y_2)^2\right)+\right.\right.\right.\\ &\left.\left.\left.(a-b)(a+b) (-(x_1-x_2+y_1-y_2) (x_1-x_2-y_1+y_2) \cos\,2\alpha-2 (x_1-x_2) (y_1-y_2) \sin\,2\alpha)\right)/\right.\right.\\ &\left.\left.\left(-\left(a^2+b^2\right) \left((x_1-x_2)^2+(y_1-y_2)^2\right)+(a-b) (a+b) ((x_1-x_2+y_1-y_2) (x_1-x_2-y_1+y_2) \cos\,2\alpha+\right.\right.\right.\\ &\left.\left.\left.2(x_1-x_2)(y_1-y_2)\sin\,2\alpha)\right)\right)\right) \end{align*}$$

Answer 4

Unfortunately, my correction on the answer of whuber has been rejected, but I'll try to explain it here.

The chosen answer is very good, but there is an error. $c$ is supposed to be the distance from point $M$ to point $R_1$. The points $R_1$ and $R_2$ are then converted into $S_1$ and $S_2$, respectively, whereby $S_2 = -S_1$. Each $S_1$ and $S_2$ are of length c, as is correctly stated. So the value of c is actually $$c = ||S_1 - S_2||/2 = ||2S_1||/2 = ||S_1||$$ apposed to $c \neq ||S_1||/2$.

It occurred to me while trying to implement the proposed solution. Using this correction, the formula works as expected.