Starting with,
$$x^3+y^3+z^3 = (z+1)^3$$
we do the substitution $z = 3 n^2x + (3 n^2 + 1)(y - 1)$ like Adam Bailey in this post to get the ellipse,
$$x^2 - x y + y^2 - (27 n^4 - 1) x - (27n^4 + 18 n^2 + 2 ) y + (27n^4 + 9 n^2 + 1 ) = 0$$
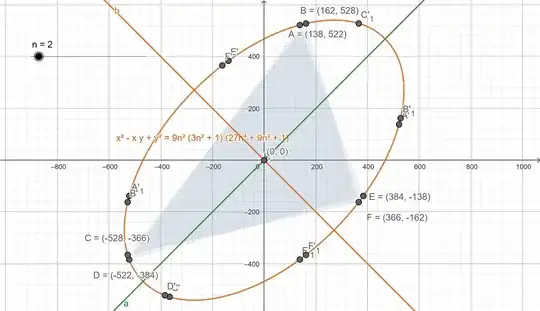
after removing a trivial factor. For general integer $n$, this family of ellipses seems to have nice properties. The case $n=1$ was in the linked post. For $n=2$,
$$x^2 - x y + y^2 - 431 x - 506 y + 469 = 0$$
which yields the ellipse,
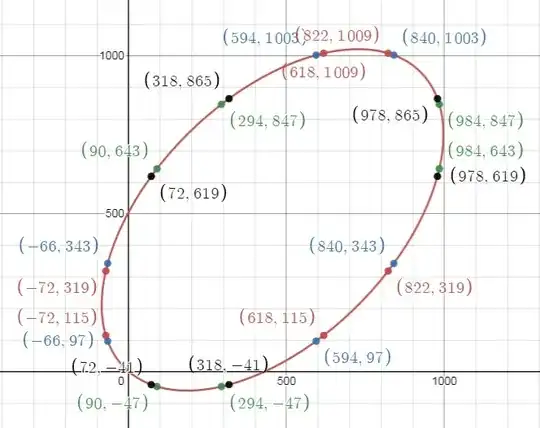
graphed by the Desmos calculator. Using the $6$ blue lattice points (and flipping $x,y$ as needed), we get the nice $6$-cycle of equalities,
\begin{align} \color{blue}{(-66)}^3\; +\; \color{blue}{97}^3 + 456^3 &= 457^3\\ \color{blue}{97}^3\; +\; \color{blue}{594}^3 + 8376^3 &= 8377^3\\ \color{blue}{594}^3 + \color{blue}{1003}^3 + 20154^3 &= 20155^3\\ \color{blue}{1003}^3 + \color{blue}{840}^3 + 23106^3 &= 23107^3\\ \color{blue}{840}^3 + \color{blue}{343}^3 + 14526^3 &= 14527^3\\ \color{blue}{343}^3 + (-66)^3 + 3654^3 &= 3655^3\end{align}
thus the sextuple $a_i = (-66, 97, 594, 1003, 840, 343)$ and similarly for the given $24$ lattice points. But the Alpertron calculator says this ellipse has a total of $48$, with the others being,
So we in fact have $48/6 = 8$ sextuples,
\begin{align}a_i & = (-66, 97, 594, 1003, 840, 343)\\ b_i & = (-72, 115, 618, 1009, 822, 319)\\ c_i & = (90, -47, 294, 847, 984, 643)\\ d_i & = (72, -41, 318, 865, 978, 619)\\ e_i & = (-78, 139, 648, 1015, 798, 289)\\ f_i & = (264, 823, 990, 673, 114, -53)\\ g_i & = (-42, 49, 522, 979, 888, 415)\\ h_i & = (24, -17, 390, 913, 954, 547)\end{align}
each one yielding a sextuple system $x^3+y^3+z^3 =(z+1)^3$ as demonstrated above for $a_i$. But notice the curious relationship,
$$\alpha = a_1 + a_3 + a_5 = b_1 + b_3 + b_5 = \dots = h_1 + h_3 + h_5 = 1368$$
$$\beta = a_2 + a_4 + a_6 = b_2 + b_4 + b_6 = \dots = h_2 + h_4 + h_6 = 1443$$
Question: Using the theory of conic sections, what is the geometric interpretation of \begin{align}\alpha &= 3(27n^4+6n^2)\\ \beta &= 3(27n^4+12n^2+1)\end{align} and why is it invariant using different lattice points?
P.S. For this family, I've tested it with other $n$ and the same relationship seems to hold.
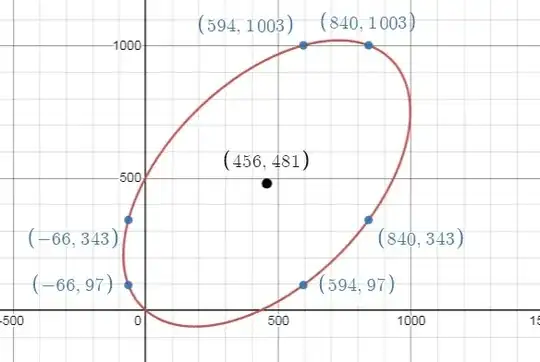
Addendum: As Jan-Magnus pointed out in his answer $\big(\dfrac{\alpha}3,\dfrac{\beta}3\big)$ should be the center of the ellipse. So,
\begin{align} \alpha &= a_1 + a_3 + a_5 = -66 + 594 + 840 = 1368 = 3\times456\\ \beta &= a_2 + a_4 + a_6 = \;97 + 1003 + 343 = 1443 = 3\times481\end{align}
Yup, looks like $(456,481)$ is indeed the center.