16

Studying past exam problems for my exam in ~$4$ weeks, and I came across this derivative as one of the questions. I actually have no idea how to solve it.

$$\frac{d}{dx} (x^{x^2})$$

Using the chain rule on it letting $x^2 = u$ led to me getting $2x^{x^2-2}$, which isn't right. The function acts like $e^x$ so I am thinking I have to convert it to this form.

So I took it to be: $$\frac{d}{dx} (e^{{x^2}log(x)})$$ Not really sure where to go from here, or if I am going in the right direction.

Gottfried Helms
  • 34,920
Display Name
  • 1,443
  • 1
  • 20
  • 45

4 Answers4

15

Yes, you've done it correctly so far, and could proceed by the chain rule.

On the other hand, set

$$y = x^{x^2}$$

Then $\ln{y} = x^2 \ln{x}$; taking a derivative on both sides and using the chain rule for the left leads to

$$\frac{y'}{y} = 2x \ln{x} + \frac{x^2}{x}$$

  • 1
    Implicit differentiation should be taught alongside the chain rule. It's so useful in situations like this, and it's the basis of a lot of the "tricks" used to solve differential equations. – Arthur Oct 18 '13 at 10:40
  • @Arthur I agree very much. – KKZiomek Apr 26 '16 at 04:45
6

Hint:

$$\frac{d}{dx} (e^{{x^2}log(x)})=\frac{d}{dx}\left({{x^2}log(x)}\right)e^{{x^2}log(x)}$$

$$\frac{d}{dx} (e^{{x^2}log(x)})=\frac{d}{dx}\left({{x^2}log(x)}\right)e^{{x^2}log(x)}=\left(x+2x\log x \right)(e^{{x^2}log(x)})$$

M.H
  • 11,498
  • 3
  • 30
  • 66
5

First, we think back to when we learned how to differentiate $x^n$, and write $\frac{d}{dx} x^{x^2} = x^2 x^{x^2 -1} = x^{x^2+1}$.

But oh no! Later we learned how to differentiate $c^x$ as $\operatorname{log}c \cdot c^x$! So let's do it that way, making sure to remember the chain rule: $\frac{d}{dx} x^{x^2} = 2x \log x \cdot x^{x^2}$.

Still, we know that neither of those answers can be right. So we'll just write them both down, and hope we get partial credit: $\frac{d}{dx} x^{x^2} = x^{x^2+1} + 2x \log x \cdot x^{x^2}$.

Andrew Dudzik
  • 30,074
2

I also first try to express the exponentiation in $y = x^{x^2}$ with the exponential function, because I can remember the derivation rules here better. :-)

Taking the natural logarithm both sides of the equation, we get $\ln y = x^2 \ln x$ and then inverting it again, we have $y = e^{x^2 \ln x}$. That is how far you got.

Now we use the chain rule:

$y' = e^{x^2 \ln x} \left(x^2 \ln x\right)'$ and then

$y' = e^{x^2 \ln x} \left(2 x \ln x + x^2 \frac{1}{x} \right)$ which gives

$y' = x^{x^2} \left(2 x \ln x + x \right)$ and finally

$y' = x^{x^2 + 1} \left(2 \ln x + 1 \right)$.

This is similiar to the answer by user T. Bongers, if you resubstitute $y = x^{x^2}$ in his answer and do a bit of combining the terms.

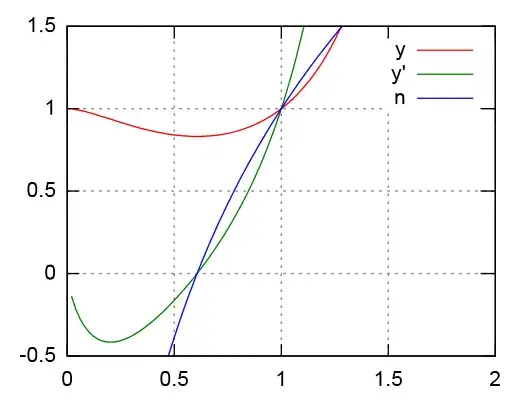
Using the übercool JavaScript port of Gnuplot at http://gnuplot.respawned.com/, where I paste 

set terminal svg enhanced size 400,300
set output 'out.svg'
set grid
plot [0:2][-0.5:1.5] exp(x*x*log(x)) title "y", exp((x*x+1) * log(x)) \
* (2 * log(x) + 1) title "y'", 2 * log(x) + 1 title "n"

I get this nice graph:

enter image description here

If you read until here I thank you. For me it was my first post here and i am amazed about the expressive features (formulas, graphs) here.

Community
  • 1
mvw
  • 34,562
  • I don't think you can even define $x^{x^2}$ for $x<0$, so taking the limit from the left doesn't make sense. How you define it for $x=0$ is immaterial, but if you want a continuous function, then the value should be $1$. – egreg Oct 18 '13 at 10:30
  • 1
    I need a couple of minutes to finish the post. I don't know what the best strategy is to prepare a longer post with some backup in between. :-) – mvw Oct 18 '13 at 10:36
  • @mvw It backs up as you write. Take a few seconds break and it should tell you (next to the "Post Your Answer" button) that the draft was saved. – Vedran Šego Oct 18 '13 at 10:52
  • 1
    @mvw If you consider a different function, then you can write whatever you want. The expression $x^{x^2}$ is not defined for $x\le0$. – egreg Oct 18 '13 at 11:05
  • @egreg I think it is defined, but on the other hand it is probably not worth too much bothering. I did consider it more because of the graphs, the derivative I think is zero at zero, looking at them. I am too lazy to look at this analyticaly (L'Hôpital or such). – mvw Oct 18 '13 at 11:30
  • @egreg See http://math.stackexchange.com/questions/415141/is-there-a-problem-when-defining-exponential-with-negative-base that the idea is not gaga. Looks like it is less pain in the complex domain, and again it is probably not that useful. – mvw Oct 18 '13 at 12:16
  • @mvw The problem is what value you take: the complex exponential $x^y$ is “multivalued” and there's no sensible way to make it one valued, unless $x$ is positive real. – egreg Oct 18 '13 at 12:18
  • OK, I edit that part out and have a look again into my old text on function theory / complex analysis. – mvw Oct 18 '13 at 12:28