9

I have a cubic Bezier curve, and I need to divide it and create same curve between point on the original curve and the end point of the original curve.

From my research, I found the DeCasteljau algorithm helps in doing this. But, to use this algorithm, I need to know the '$t$' value at the dividing point.

Can anyone please help me out to find '$t$' at a given point on a cubic Bezier curve

I need to find the value of '$t$' at a given point B.

bubba
  • 43,483
  • 3
  • 61
  • 122
Vivek Molkar
  • 193
  • 2
    It's not at all clear what you're trying to do. Can you add a diagram? – Peter Taylor Oct 15 '13 at 12:17
  • If you cannot add a diagram, a more thorough description of what you are trying to do would really help others understand the question. – Carl Mummert Oct 15 '13 at 12:50
  • He has a point on a cubic Bezier curve, and he wants to find the corresponding parameter value, $t$. This parameter value is needed as input to the de Casteljau algorithm, which he wants to use to divide the curve at the given point. Seems pretty clear to me. – bubba Oct 16 '13 at 00:33
  • If the question is re-opened, I would be happy to answer it for you. One approach is just brute-force numerical root-finding. The more clever approach uses resultants and "inversion". See sections 17.4 through 17.6 of these notes: http://cagd.cs.byu.edu/~557/text/ch17.pdf. – bubba Oct 16 '13 at 00:46
  • Actually, there are two "inversion" algorithms. They are described on pages 200-202 of the reference I gave above. – bubba Oct 16 '13 at 04:42
  • There is a description of how to divide a Bezier curve in this topic: http://math.stackexchange.com/questions/317806/equation-for-subsection-of-bezier-curve?rq=1 – bubba Oct 16 '13 at 04:48
  • How does one get a point on the Bezier curve without the t parameter? I mean you need the t for any point on the curve, if you have a t you can divide it at t. How does one know a point on the curve, without at one time having known the value for t for that point? – Tatarize Jul 11 '16 at 12:41

2 Answers2

9

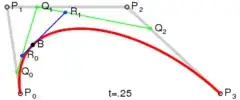
Suppose we let $\mathbf{P}(t)$ be the Bezier curve, and let the given point be $\mathbf{B}$.

In theory, we want to find a value of $t$ such that $\mathbf{P}(t) = \mathbf{B}$. If you write out the $x$ and $y$ components separately, this will give you two cubic equations, which should have a common root, $t$.

But, in floating point arithmetic, $\mathbf{B}$ will be some small distance away from the curve, and we need to accomodate this. So, a better approach is to find the point on the curve that is closest to $\mathbf{B}$. In other words, find the value of $t$ that minimises the distance from $\mathbf{B}$ to $\mathbf{P}(t)$. At the point where this happens, the vector $\mathbf{P}(t) - \mathbf{B}$ will be perpendicular to the curve tangent, so $$ (\mathbf{P}(t) - \mathbf{B}) \cdot \mathbf{P}'(t) = 0 $$ Since $\mathbf{P}(t)$ is cubic and $\mathbf{P}'(t)$ is quadratic, this is an equation of degree 5 in $t$, which you can solve using your favorite numerical root-finder. This is the brain-dead brute force approach.

Now a smarter way ...

If you look in these notes by Tom Sederberg, you will find some techniques for "inversion" of polynomial and rational curves, based on the use of resultants. Specifically, on page 204, you will find a formula for doing "inversion" of a cubic curve written in Bezier form, and there's a nice worked example on page 205. This is exactly what you need.

As I mentioned above, you will often meet cases where the given point $\mathbf{B}$ is not exactly on the curve. You can apply the inversion formula, anyway, and it will give you some value of $t$. I'm not 100% sure what point this value of $t$ represents. I don't think it's the point on the curve that's closest to $\mathbf{B}$, but it should be good enough if $\mathbf{B}$ is already very close to the curve.

bubba
  • 43,483
  • 3
  • 61
  • 122
2

This is function for cubic bezier

$p = p_0(1 - t)^3 + 3p_1t(1 - t)^2 + 3p_2t^2(1 - t) + p_3t^3$

It can be reaarange into

$ p = p_0(1 - 3t + 3t^2 - t^3) + 3p_1(t - 2t^2 + t^3) + 3p_2(t^2 - t^3) + p_3t^3 \\ t^3(p_3 - 3p_2 + 3p_1 - p_0) + t^23(p_2 - 2p_1 + p_0) + t3(p_1 - p_0) + p_0 - p = 0 $

From this point it's a cubic equation for $x$ and $y$

You can find $t$ from $x$ and cubic equation will result in 3 possible values. Then you put $t$ back into function to get 3 $y$ and select a value close to the $y$ you put in

Thaina
  • 672