5

I have a Bézier cubic curve $P$, and I would like to know what the equation of its tangent to the point $A$, where $A$ is any point of the curve.

I know the coordinates of the four points of the curve and the coordinates of the point $A$.

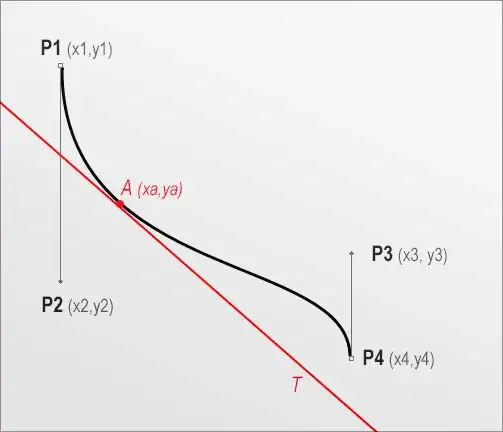
See my graphic : Tangent to Bezier Cubic Curve

Nicolas Bocquel
  • 51
  • Find a way to write the curve in parametric from $x(t), y(t)$, then the tangent equation in parametric form is $x'(t) = \frac{dx}{dt}, y'(t) = \frac{dy}{dt}$ – Blex Sep 05 '17 at 09:13
  • ...but since this tangent is a straight line, I rather look for an affine function with a cartesian equation (y=ax+b).. :-) – Nicolas Bocquel Sep 05 '17 at 10:26
  • You know $A$ but not the corresponding $t\in [0,1]$ ? – lhf Sep 05 '17 at 11:44
  • @lhf : no, I do not know "t", but if I have all the coordinates of all the points, I suppose it does not have to be complicated to get "t" with the polynomial function of Bernstein . – Nicolas Bocquel Sep 05 '17 at 14:04
  • See https://math.stackexchange.com/questions/527005/find-value-of-t-at-a-point-on-a-cubic-bezier-curve. – lhf Sep 05 '17 at 18:03
  • Very interesting. Thanks. – Nicolas Bocquel Sep 05 '17 at 20:37
  • If you can find $t$, then see https://en.wikipedia.org/wiki/Bézier_curve#Derivative. – amd Sep 06 '17 at 08:23

1 Answers1

1

If you know the value of the four points, then the parametric equation for curve P is found through the following: $$\left(\left(1-t\right)\left(\left(1-t\right)\left(\left(1-t\right)x_{1}+tx_{2}\right)+t\left(\left(1-t\right)x_{2}+tx_{3}\right)\right)+t\left(\left(1-t\right)\left(\left(1-t\right)x_{2}+tx_{3}\right)+t\left(\left(1-t\right)x_{3}+tx_{4}\right)\right),\left(1-t\right)\left(\left(1-t\right)\left(\left(1-t\right)y_{1}+ty_{2}\right)+t\left(\left(1-t\right)y_{2}+ty_{3}\right)\right)+t\left(\left(1-t\right)\left(\left(1-t\right)y_{2}+ty_{3}\right)+t\left(\left(1-t\right)y_{3}+ty_{4}\right)\right)\right)$$ where the domain of $t$ is $[0,1]$ This gives us $$x_{t}=x_{1}-3\left(x_{1}-x_{2}\right)t+3t^{2}\left(x_{1}-2x_{2}+x_{3}\right)-t^{3}\left(x_{1}-3x_{2}+3x_{3}-x_{4}\right)$$ $$y_{t}=y_{1}-3\left(y_{1}-y_{2}\right)t+3t^{2}\left(y_{1}-2y_{2}+y_{3}\right)-t^{3}\left(y_{1}-3y_{2}+3y_{3}-y_{4}\right)$$ You want the $y=mx+b$ formula for the line passing through the point $(x_a,y_a)$. Any $(x_a,y_a)$ value obtained through the above formula has a corresponding slope given by the set of parametric equations $x_t=x_t$ and $y'_t=\frac{\frac{d}{dt}{y_t}}{\frac{d}{dt}{x_t}}$ This gets us the following: $$x_{t}=x_{1}-3\left(x_{1}-x_{2}\right)t+3t^{2}\left(x_{1}-2x_{2}+x_{3}\right)-t^{3}\left(x_{1}-3x_{2}+3x_{3}-x_{4}\right)$$ $$y'_{t}=\frac{-\left(3\left(y_{1}-y_{2}\right)-6t\left(y_{1}-2y_{2}+y_{3}\right)+3t^{2}\left(y_{1}-3y_{2}+3y_{3}-y_{4}\right)\right)}{-\left(3\left(x_{1}-x_{2}\right)-6t\left(x_{1}-2x_{2}+x_{3}\right)+3t^{2}\left(x_{1}-3x_{2}+3x_{3}-x_{4}\right)\right)}$$ $$y'_{t}=\frac{\left(y_{1}-y_{2}\right)-2t\left(y_{1}-2y_{2}+y_{3}\right)+t^{2}\left(y_{1}-3y_{2}+3y_{3}-y_{4}\right)}{\left(x_{1}-x_{2}\right)-2t\left(x_{1}-2x_{2}+x_{3}\right)+t^{2}\left(x_{1}-3x_{2}+3x_{3}-x_{4}\right)}$$ This gives you the slope of the line. With a point and a slope, we can develop our linear equation. $$y-y_{t}=y'_{t}\left(x-x_{t}\right)$$ $$y=y'_{t}x-y'_{t}\left(x_{t}\right)+y_{t}$$ $$y=\frac{\frac{d}{dt}y_{t}}{\frac{d}{dt}x_{t}}x-\frac{\frac{d}{dt}y_{t}}{\frac{d}{dt}x_{t}}x_{t}+y_{t}$$ But if you want to brute force an equation, here is an expanded version of that. $$y=\frac{\left(y_{1}-y_{2}\right)-2t\left(y_{1}-2y_{2}+y_{3}\right)+t^{2}\left(y_{1}-3y_{2}+3y_{3}-y_{4}\right)}{\left(x_{1}-x_{2}\right)-2t\left(x_{1}-2x_{2}+x_{3}\right)+t^{2}\left(x_{1}-3x_{2}+3x_{3}-x_{4}\right)}x-\frac{\left(y_{1}-y_{2}\right)-2t\left(y_{1}-2y_{2}+y_{3}\right)+t^{2}\left(y_{1}-3y_{2}+3y_{3}-y_{4}\right)}{\left(x_{1}-x_{2}\right)-2t\left(x_{1}-2x_{2}+x_{3}\right)+t^{2}\left(x_{1}-3x_{2}+3x_{3}-x_{4}\right)}\left(x_{1}-3\left(x_{1}-x_{2}\right)t+3t^{2}\left(x_{1}-2x_{2}+x_{3}\right)-t^{3}\left(x_{1}-3x_{2}+3x_{3}-x_{4}\right)\right)+y_{1}-3\left(y_{1}-y_{2}\right)t+3t^{2}\left(y_{1}-2y_{2}+y_{3}\right)-t^{3}\left(y_{1}-3y_{2}+3y_{3}-y_{4}\right)$$ At any value t from 0 to 1, that will be your tangent line passing through the point $(x_{1}-3\left(x_{1}-x_{2}\right)t+3t^{2}\left(x_{1}-2x_{2}+x_{3}\right)-t^{3}\left(x_{1}-3x_{2}+3x_{3}-x_{4}\right),y_{1}-3\left(y_{1}-y_{2}\right)t+3t^{2}\left(y_{1}-2y_{2}+y_{3}\right)-t^{3}\left(y_{1}-3y_{2}+3y_{3}-y_{4}\right))$

Joseph Gatts
  • 111