A simple question about sine and cosine

Question

I have been thinking about all of the different ways that I have encountered sine and cosine in my studies. There are no courses on trigonometry at my school, so perhaps that's why I feel like something is missing, something that ties all of these ideas together.

• The Unit Circle. The unit circle is a way to organize all possible right triangles up to similarity. The sine and cosine can be defined as ratios of sides of these right triangles, though in practice the sine becomes the vertical component and the cosine the horizontal. What I want to know is how do I relate this beautiful diagram to the other constructions of sine and cosine.

• The orthonormal basis of the solution space to the differential equation: $y'' = -y$. In some sense this is as good of a definition as the unit circle.

• Taylor Series. These grow clearly out of the differential equation above. How could I connect Taylor series to the concept of the unit circle? I think of partial Taylor series as "better and better" approximations of these function centered at zero (or maybe some place else, I guess it would not matter) -- so how is that concept linked to what $y'' = -y$ says about these equations?

Lastly, are there any other major representations I should also consider?

Answer 1

It all comes down to representation theory. The assignment $\theta \mapsto \left[ \begin{array}{cc} \cos \theta & - \sin \theta \\\ \sin \theta & \cos \theta \end{array} \right]$ sending an angle $\theta$ to a matrix describing rotation by $\theta$ in the Euclidean plane $\mathbb{R}^2$ is a group homomorphism, so abstractly one cay say that sine and cosine naturally appear as matrix coefficients of this particular representation of the group $\mathbb{R}$ or perhaps instead of the circle group $S^1$.

The connection to Fourier series is given abstractly by Pontrjagin duality, which describes the representation theory of a large class of abelian groups, and the connection to differential equations is given by the fact that the space of solutions to $y'' = -y$

• naturally inherits the structure of a representation of $\mathbb{R}$ given by translation $y(x) \mapsto y(x+t)$, and
• has the property that $y^2 + (y')^2 = \text{const}$ for any solution $y$ by inspection, which is strongly suggestive of (but does not immediately prove) periodicity. Note that we get a parameterization of the unit circle this way.

The second property can be understood as conservation of energy for a harmonic oscillator and comes from the first via Noether's theorem.

Answer 2

My intuitive interpretation is usually in the terms of projections, \begin{align} x \cdot y &= |x||y|\cos(\theta) \end{align} If necessary, sine can be viewer similarly, as projected towards $y_\perp$.

Answer 3

Start with $x'' = -x$. Introduce $y = x'$, so that $$\begin{align}x' &= y, \\ y' &= x'' = -x.\end{align}$$

Now let $\mathbf x = [x, y]^T$ be the coordinates of a point in the 2D plane. Then we have $$\mathbf x'' = \begin{bmatrix}0 & 1 \\ -1 & 0\end{bmatrix} \mathbf x.$$ Assuming $\lVert \mathbf x(0) \rVert = 1$, this is the equation of a particle on the unit circle (exercise: show this) moving with unit speed (exercise: show this). (Hint: observe that the matrix in question produces a vector perpendicular to $\mathbf x$.)

Therefore,the angle $\theta$ that the particle makes with the horizontal axis increases at one radian per unit time, so $\theta = t$. From the geometrical picture, this means that the coordinates of the particle are $x(t) = \cos(t)$ and $y(t) = \sin(t)$.

In general, an $n$th-order ODE in one dimension can be thought of as a first-order ODE — a "flow" — in $n$-dimensional space. Here, the flow corresponding to $x'' = -x$ is uniform rotation around the origin in a 2D plane.

(In my view, the connection between Taylor series and the geometrical picture is only via the differential equation, and that has little do to with circles specifically. So if you don't get an answer addressing that here, I think your penultimate sentence would make a good question worth asking separately.)

Answer 4

In actuality, the best way to think of this is to think of angles traditionally, as a pair of rays sharing a common vertex. We can form an equivalence relation on angles, by saying that they are equivalent if there is a direct isometry between them. Then, we can partition all the possible angles in $\mathbb{R}^2$ into the equivalence classes, and the class of equivalence classes is a set, so it can be totally ordered. With this total ordering, the set of equivalence classes, as defined above, is order-isomorphic to the interval of real numbers $(-p,p]$ for some real number $p.$ The idea is that for each equivlance class, the real number assigned is a quantitative measure of the angles in the equivalence class. All angles in the same equivalence class have the same measure. Typically, $p$ is chosen to be equal to $\pi,$ but in actuality, $p$ is an arbitrary positive real number. A choice of $\pi$ amounts simply to a choice of half-period for the sinusoidal functions parametrizing the unit circle, with the parametrization corresponding directly to the interval $(-p,p].$

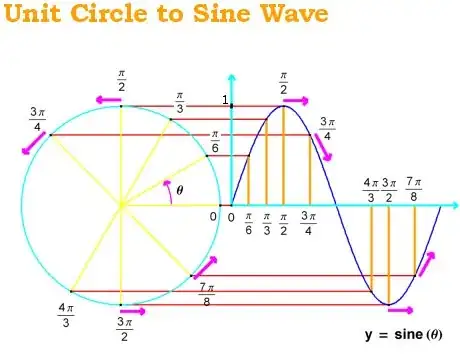
For a given choice of $p,$ the arclength of an arc corresponding to an angle measuring $s,$ where $s\in(-p,p],$ is equal to $\frac{\pi}{p}s.$ This makes the choice $p=\pi$ the most natural, and this is why people often say that doing calculus requires using radians. This is because calculus is most natural when the sinusoidal functions are chosen such that their half-period $p$ is $\pi.$ To demonstrate this point, consider the parametrization $(x(t),y(t)),$ where $x,y:(-p,p]\to[-1,1],$ such that $x$ is even, $y$ is odd, $x,y$ are continuous, and the functions satisfy the joint equation $x(t)^2+y(t)^2=1,$ and the boundary conditions $x(0)=1,$ $x(p)=-1,$ $y(0)=y(p)=0.$ This uniquely defines the sinusoidal functions $x$ and $y.$ The key idea to do calculus is the limit $$\lim_{t\to0}\frac{y(t)}{t}.$$ It can be proven, from elementary geometry, or using the unit circle parametrization, that $$x(u+v)=x(u)x(v)-y(u)y(v)$$ and $$y(u+v)=y(u)x(v)+x(u)y(v).$$ Hence $$y'(t)=\lim_{\epsilon\to0}\frac{y(t+\epsilon)-y(t)}{\epsilon}=y(t)\lim_{\epsilon\to0}\frac{x(\epsilon)-1}{\epsilon}+x(t)\lim_{\epsilon\to0}\frac{y(\epsilon)}{\epsilon}$$ and $$x'(t)=\lim_{\epsilon\to0}\frac{x(t+\epsilon)-x(t)}{\epsilon}=x(t)\lim_{\epsilon\to0}\frac{x(\epsilon)-1}{\epsilon}-y(t)\lim_{\epsilon\to0}\frac{y(\epsilon)}{\epsilon}.$$ Notice that $$\lim_{\epsilon\to0}\frac{x(\epsilon)-1}{\epsilon}=\lim_{\epsilon\to0}\frac{x(\epsilon)^2-1}{\epsilon[x(\epsilon)+1]}=-\lim_{\epsilon\to0}\frac{y(\epsilon)^2}{\epsilon[x(\epsilon)+1]},$$ and assuming $$\lim_{\epsilon\to0}\frac{y(\epsilon)}{\epsilon}$$ exists, we can safely say $$-\lim_{\epsilon\to0}\frac{y(\epsilon)^2}{\epsilon[x(\epsilon)+1]}=-\lim_{\epsilon\to0}\frac{y(\epsilon)}{x(\epsilon)+1}\lim_{\epsilon\to0}\frac{y(\epsilon)}{\epsilon}=0.$$ As for $$\lim_{\epsilon\to0}\frac{y(\epsilon)}{\epsilon},$$ we know, from the parametrization of the unit circle, that $$y(t)\leq\frac{\pi}{p}t\leq\frac{y(t)}{x(t)}$$ for $0\lt{t}\lt\frac{p}2,$ and $$y(t)\geq\frac{\pi}{p}t\geq\frac{y(t)}{x(t)}$$ for $0\gt{t}\gt-\frac{p}2.$ Dividing by $y(t)$ gives that $$1\leq\frac{\pi}{p}\frac{t}{y(t)}\leq\frac1{x(t)}$$ for $0\lt{t}\lt\left|\frac{p}2\right|.$ Therefore, $$x(t)\leq\frac{p}{\pi}\frac{y(t)}{t}\leq1,$$ hence $$\lim_{t\to0}x(t)=1\leq\frac{p}{\pi}\lim_{t\to0}\frac{y(t)}{t}\leq1.$$ This means $$\frac{p}{\pi}\lim_{t\to0}\frac{y(t)}{t}=1$$ or $$\lim_{t\to0}\frac{y(t)}{t}=\frac{\pi}{p}.$$ This gives us $$y'(t)=\frac{\pi}{p}$$ and $$x'(t)=-\frac{\pi}{p}y(t).$$ This is what connects the trigonometric definition of sine and cosine to their derivative definitions.

However, I prefer defining the trigonometric functions in terms of the inverse elliptic integrals instead, and this is more, natural, and it avoids making direct reference to $\pi.$ The elliptic integrals are covered by this article https://en.wikipedia.org/wiki/Elliptic_integral and the definition that I give of the arcsin is that of $$\arcsin(x):=E(x;0).$$ This relates it naturally to the arclength of an arc in a circle, and it also analogizes it with the definition of the natural logarithm as that of an area enclosed by a hyperbola.