Is a constant raised to the power of infinity indeterminate? I am just curious. Say, for instance, is $0^\infty$ indeterminate? Or is it only 1 raised to the infinity that is?
-
1If we type those expressions into Mathematica, however, it tells us that 0^infinity is 0 and 1^infinity is indeterminate. – Oct 09 '13 at 23:42
-
All the answers here assume $0^{\infty}$ is $0^{+\infty}$. But Wikipedia doesn't assume that. It claims that $0^{\infty}$ is an indeterminate form because $0^{+\infty}$ has the limiting value $0$, and $0^{-\infty}$ is equivalent to $1/0$, which, as talked about in the same place I linked, is "not commonly regarded as an indeterminate form because there is not an infinite range of values that $f/g$ could approach." – user236182 Sep 16 '17 at 23:47
-
"Specifically, if $f$ approaches $1$ and $g$ approaches $0$, then $f$ and $g$ may be chosen so that $(1)$ $f/g$ approaches $+\infty$, $(2)$ $f/g$ approaches $−\infty$, or $(3)$ the limit fails to exist. In each case the absolute value $|f/g|$ approaches $+\infty$, and so the quotient $f/g$ must diverge, in the sense of the extended real numbers. (In the framework of the projectively extended real line, the limit is the unsigned infinity $\infty$ in all three cases.)" – user236182 Sep 16 '17 at 23:50
-
"Similarly, any expression of the form $a/0$, with $a \neq 0$ (including $a = +\infty$ and $a = −\infty$), is not an indeterminate form since a quotient giving rise to such an expression will always diverge." – user236182 Sep 16 '17 at 23:50
3 Answers
No, it is zero.
Consider the function $f(x,y) = x^y$ and consider any sequences $\{(x_0, y_0), (x_1, y_1), \ldots\}$ with $x_i \to 0$ and $y_i \to \infty$. It is easy to see that $f(x_n,y_n)$ converges to zero: let $\epsilon > 0$. For some $N$, $|x_i| < \epsilon$ and $y_i > 1$ for all $i \geq N$, so $|f(x_i,y_i)| < \epsilon$ for all $i\geq N$.
More generally, as $x\to c$ and $y\to \infty$, $x^y$ converges to 0 for $|c|<1$, diverges to infinity for $c>1$, oscillates without converging for $c \leq -1$, and is indeterminate when $c=1$.
- 49,280
-
1Hm, why does wolfram seem to think this limit DNE? http://www.wolframalpha.com/input/?i=lim+x+-%3E0%2C+y-%3E+inf+of+x%5Ey – alecbz Oct 10 '13 at 00:24
-
1wolfram alpha tells you why with the caveat: depends on the path in complex space. – Tyler Oct 10 '13 at 00:30
-
1user7530 guessed that Skylion intended "positive reals" for $x$ and $y$. Wolfram Alpha guessed that it means a limit for $x,y$ in the complex plane. Only Skylion can tell us what she meant. – GEdgar Oct 10 '13 at 00:32
-
1Because the question is ambiguous: Mathematica, as it implies, interprets it as a limit of the complex exponential. This is very different than user7530's interpretation as an operation on the extended real numbers, where the limit used to compute it is restricted to positive bases and real exponents. – Oct 10 '13 at 00:33
-
Yes, I assumed that $x$ and $y$ are real, and $\infty$ is the positive real infinity. For complex numbers, it's also true that $x^y\to 0$ as $|x|\to 0$ and $y\to \infty$, where again here I mean the positive real infinity. – user7530 Oct 10 '13 at 00:37
-
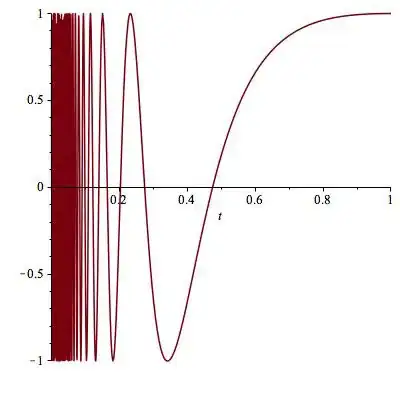
Since the question came to the front page again, let's do a complex example, to show that (at least this time) Mathematica is not crazy...
For $t>0$, let $f(t) = t, g(t) = i/t$. Then
$$
\lim_{t\to 0+} f(t) = 0,\qquad \lim_{t\to 0+}g(t) = \infty
\\
f(t)^{g(t)} = \exp\frac{i\;\log t}{t}
$$
and $\mathrm{Re} \Big(f(t)^{g(t)}\Big)$ (pictured) does not converge as $t \to 0^+$.
- 111,679
Any constant raised to the power $\infty$ or $\infty$ raised to the power of any constant is undoubtedly always indeterminate. This is because exponentiation $x^y$ is a binary operation from $\mathbb{S} \times \mathbb{S} \to \mathbb{S}$, where $\mathbb{S}$ is a set such that $x, y, x^y \in \mathbb{S}$. To the best of my knowledge, $\infty$ doesn't belong to any known set of numbers, which itself means neither $x$ nor $y$ can ever be $\infty$. That is to say, both $x^\infty$ and $\infty^y$ are indeterminate. Therefore, it follows that both $0^\infty$ and $1^\infty$ are indeterminate.
EDIT: Some people in the comments section are saying $1^\infty =1 $ and $0^\infty = 0$ by taking the help of limits. $\displaystyle \lim_{x\to\infty} 1^x$ is not the same as $1^\infty$. The former gives an approximate value of $1^x$ when $x$ is very close to $\infty$, but $x$ is still defined. Obviously, $\displaystyle \lim_{x\to\infty} 1^x = 1$ but $1^\infty \neq 1$. Both of them have different meanings. Same applies to the case of $0^\infty$ too. The question does not mention anything about limits. So the answer assumes that exact values of $1^\infty$ and $0^\infty$ are being referred to, which are absolutely indeterminate.
- 11
-
I see your point but your conclusion is not necessarily true. You are correct in saying that $\infty$ is not a number but there are other interpretations of the expression $0^{\infty}$ and $1^{\infty}$. Aside from the answers given below we also view $x^y$ as the number of functions from a set of size $y$ to a set of size $x$. There are no functions from an infinite set to the empty set and there is only one function from an infinite set to a singleton set. In that interpretation $0^{\infty}=0$ and $1^{\infty}=1$. – John Douma Oct 12 '22 at 17:32
-
@JohnDouma When different mathematical interpretations of the same thing are not in agreement, then it's best not to interpret them mathematically at all. Those things are left out to be analyzed by the philosophers, not mathematicians. There is no rigourous mathematical explanation for the indeterminate forms (although I have attempted to provide one), hence the name. – ArijitKD Oct 12 '22 at 18:24
-
That's just it. The different interpretations agree. By your example, $\Sigma_{i=0}^{\infty}\text{something}$ would be indeterminate too. – John Douma Oct 12 '22 at 18:44
-
(-1) This answer is very incorrect. An indeterminate form can be understood as an expression representing all possible limits of an operation performed on functions. That is, for some operation $$, the indeterminate form $ab$ denotes $\lim_x [f(x)*g(x)]$ where $\lim_x f(x)=a$ and $\lim_x g(x)=b$ and $f,g$ are real-valued functions of real variables. If $f\to0$, $g\to\infty$, then $f^g\to 0$, so we may write $0^\infty=0$. It does not matter that $\infty$ is not in the real numbers. – Jam Oct 12 '22 at 19:26
-
@JohnDouma Of course, it is indeterminate. The summation notation that you show is actually $\displaystyle \lim_{n\to\infty} \sum^n_{x=0} f(x)$ and not simply $\displaystyle \sum^\infty_{x=0} f(x)$. In the former case the sum is defined because $x\to\infty$ but $x\neq\infty$. In the latter case, the summation assumes that $x=\infty$ is the upper bound which cannot be true. Although the latter form is widely used, technically it's incorrect in its sense. – ArijitKD Oct 13 '22 at 05:39
-
@Jam No it's not incorrect. You are considering the values when the limits are being taken. The question was about simply $1^\infty$ and $0^\infty$. $\displaystyle \lim_{x\to\infty} 1^x$ is not same as $1^\infty$. Same applies to the $0^\infty$ case too. When limits are taken, all indeterminate forms are always defined. Precisely stated, $\displaystyle \lim_{x\to\infty} 1^x \approx 1$ but $\neq 1$ and $\displaystyle \lim_{x\to\infty} 0^x \approx 0$ but $\neq 0$. – ArijitKD Oct 13 '22 at 05:56
-
@MisterTux You are misunderstanding what indeterminate forms are and seem to be confusing indeterminate with undefined. Please read Sec 4.4 of Stewart's calculus and MathWorld: Indeterminate. The forms $1^\infty$ and $\frac00$ are indeterminate since limits of these forms could approach any value. The forms $0^\infty=0$ and $\frac10=\pm\infty$ are not indeterminate since limits of those forms will always approach certain values. (1/2) – Jam Oct 13 '22 at 08:12
-
Expressions representing undefined arithmetic operations in the real numbers are not necessarily indeterminate forms, as the other answers on this page demonstrate. See MSE Q554521. You are also clearly misunderstanding what limits are. They are exact, not approximations. This is the same fallacy that makes people claim that $0.999\ldots$ is approximately equal to $1$ despite that they are exactly the same number. See MSE Q11. (2/2) – Jam Oct 13 '22 at 08:17